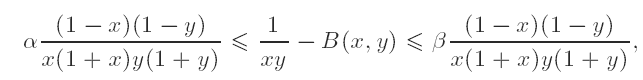Refine search
Actions for selected content:
25846 results in Abstract analysis
Introduction
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp vii-xii
-
- Chapter
- Export citation
7 - Dynamical Rigidity of CIFSs
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 171-208
-
- Chapter
- Export citation
8 - Parabolic Iterated Function Systems
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 209-237
-
- Chapter
- Export citation
5 - Examples of GDMSs
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 136-143
-
- Chapter
- Export citation
2 - Symbolic Dynamics
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 4-53
-
- Chapter
- Export citation
1 - Preliminaries
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 1-3
-
- Chapter
- Export citation
Appendix 2 - Geometric measure theory
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 264-268
-
- Chapter
- Export citation
Index
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 280-281
-
- Chapter
- Export citation
Contents
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp v-vi
-
- Chapter
- Export citation
Appendix 1 - Ergodic theory
-
- Book:
- Graph Directed Markov Systems
- Published online:
- 14 August 2009
- Print publication:
- 07 August 2003, pp 262-263
-
- Chapter
- Export citation
Qualitative analysis of a ratio-dependent predator–prey system with diffusion
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 919-942
- Print publication:
- August 2003
-
- Article
- Export citation
The initial–boundary-value problem for real viscous heat-conducting flow with shear viscosity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 969-986
- Print publication:
- August 2003
-
- Article
- Export citation
ON MULTIPLICATION TABLES OF GROUPS THAT AGREE ON HALF OF THE COLUMNS AND HALF OF THE ROWS
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 2 / May 2003
- Published online by Cambridge University Press:
- 01 August 2003, pp. 293-308
-
- Article
-
- You have access
- Export citation
A Hölder continuous ODE related to traffic flow
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 759-772
- Print publication:
- August 2003
-
- Article
- Export citation
Homogenization of a Hamilton–Jacobi equation associated with the geometric motion of an interface
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 773-805
- Print publication:
- August 2003
-
- Article
- Export citation
Stability of scalar delay differential equations with dominant delayed terms
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 951-968
- Print publication:
- August 2003
-
- Article
- Export citation
Pencils of differential operators containing the eigenvalue parameter in the boundary conditions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 893-917
- Print publication:
- August 2003
-
- Article
- Export citation
Uniform asymptotic expansions for associated Legendre functions of large order
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 807-827
- Print publication:
- August 2003
-
- Article
- Export citation
Estimates of averages of Fourier transforms with respect to general measures
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 943-950
- Print publication:
- August 2003
-
- Article
- Export citation
Some beta-function inequalities
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 4 / August 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 731-745
- Print publication:
- August 2003
-
- Article
- Export citation