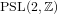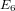Refine search
Actions for selected content:
2540 results in Computational Science
Acknowledgments
-
- Book:
- Teaching Computational Creativity
- Published online:
- 04 July 2017
- Print publication:
- 02 May 2017, pp xxi-xxii
-
- Chapter
- Export citation
7 - Design Scenes of Online Code Learning Environments
- from PART IV - ONLINE LEARNING
-
-
- Book:
- Teaching Computational Creativity
- Published online:
- 04 July 2017
- Print publication:
- 02 May 2017, pp 163-190
-
- Chapter
- Export citation

Arithmetical Wonderland
-
- Published by:
- Mathematical Association of America
- Published online:
- 27 April 2017
- Print publication:
- 30 October 2015
-
- Book
- Export citation
Treatment for third-order nonlinear differential equations based on the Adomian decomposition method
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 20 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 01 April 2017, pp. 1-10
-
- Article
-
- You have access
- Export citation
Picard curves over
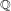 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
Certain aspects of holomorphic function theory on some genus-zero arithmetic groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 360-381
-
- Article
-
- You have access
- Export citation

Volterra Integral Equations
- An Introduction to Theory and Applications
-
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017
5 - Singularly Perturbed and Integral-Algebraic Volterra Equations
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 198-222
-
- Chapter
- Export citation
Contents
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp v-x
-
- Chapter
- Export citation
Appendix - A Review of Banach Space Tools
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 325-343
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp i-iv
-
- Chapter
- Export citation
1 - Linear Volterra Integral Equations
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 1-56
-
- Chapter
- Export citation
8 - Volterra Integral Operators on Banach Spaces
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 279-303
-
- Chapter
- Export citation
References
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 344-382
-
- Chapter
- Export citation
4 - Volterra Integral Equations with Highly Oscillatory Kernels
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 175-197
-
- Chapter
- Export citation
2 - Regularity of Solutions
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 57-102
-
- Chapter
- Export citation
7 - Cordial Volterra Integral Equations
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 241-278
-
- Chapter
- Export citation
Preface
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp xi-xvi
-
- Chapter
- Export citation
9 - Applications of Volterra Integral Equations
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 304-324
-
- Chapter
- Export citation
6 - Qualitative Theory of Volterra Integral Equations
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 223-240
-
- Chapter
- Export citation