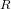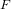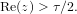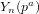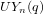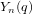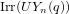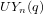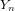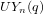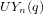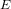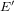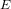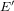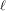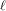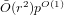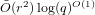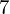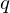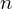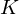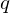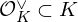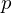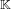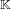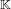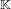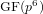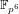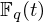Refine search
Actions for selected content:
2540 results in Computational Science
3 - Non-Linear Volterra Integral Equations
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 103-174
-
- Chapter
- Export citation
Index
-
- Book:
- Volterra Integral Equations
- Published online:
- 02 February 2017
- Print publication:
- 20 January 2017, pp 383-387
-
- Chapter
- Export citation
On the double Laplace transform of the truncated variation of a Brownian motion with drift
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 281-292
-
- Article
-
- You have access
- Export citation
Analysis of semilocal convergence for ameliorated super-Halley methods with less computation for inversion
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 293-302
-
- Article
-
- You have access
- Export citation
On a Li-type criterion for zero-free regions of certain Dirichlet series with real coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 259-280
-
- Article
-
- You have access
- Export citation
On the characters of the Sylow
 $p$ -subgroups of untwisted Chevalley groups
$p$ -subgroups of untwisted Chevalley groups 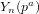 $Y_{n}(p^{a})$
$Y_{n}(p^{a})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 303-359
-
- Article
-
- You have access
- Export citation
Effective Hasse principle for the intersection of two quadrics
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 73-82
-
- Article
-
- You have access
- Export citation
Databases of elliptic curves ordered by height and distributions of Selmer groups and ranks
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 351-370
-
- Article
-
- You have access
- Export citation
Explicit isogenies in quadratic time in any characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 267-282
-
- Article
-
- You have access
- Export citation
Visualizing elements of order
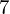 $7$ in the Tate–Shafarevich group of an elliptic curve
$7$ in the Tate–Shafarevich group of an elliptic curve
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 100-114
-
- Article
-
- You have access
- Export citation
On error distributions in ring-based LWE
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 130-145
-
- Article
-
- You have access
- Export citation
Tuple lattice sieving
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 146-162
-
- Article
-
- You have access
- Export citation
Point counting on K3 surfaces and an application concerning real and complex multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 12-28
-
- Article
-
- You have access
- Export citation
Computing Jacobi forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 205-219
-
- Article
-
- You have access
- Export citation
Computing canonical heights on elliptic curves in quasi-linear time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 391-405
-
- Article
-
- You have access
- Export citation
Reducing number field defining polynomials: an application to class group computations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 315-331
-
- Article
-
- You have access
- Export citation
Fast heuristic algorithms for computing relations in the class group of a quadratic order, with applications to isogeny evaluation
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 371-390
-
- Article
-
- You have access
- Export citation
Collecting relations for the number field sieve in
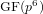 $\text{GF}(p^{6})$
$\text{GF}(p^{6})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 332-350
-
- Article
-
- You have access
- Export citation
Division algebras and maximal orders for given invariants
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 178-195
-
- Article
-
- You have access
- Export citation
A database of genus-2 curves over the rational numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 235-254
-
- Article
-
- You have access
- Export citation