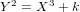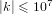Refine search
Actions for selected content:
2540 results in Computational Science
Dedication
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp v-vi
-
- Chapter
- Export citation
Appendix D - Image Credits
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 231-232
-
- Chapter
- Export citation
Appendix B - Mathematical Preliminaries
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 217-228
-
- Chapter
- Export citation
Index
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 253-254
-
- Chapter
- Export citation
5 - Higher-Order PDE Inpainting
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 63-136
-
- Chapter
- Export citation
9 - Applications
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 180-210
-
- Chapter
- Export citation
Glossaries
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 233-236
-
- Chapter
- Export citation
2 - Overview of Mathematical Inpainting Methods
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 8-25
-
- Chapter
- Export citation
Appendix A - Exercises
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 211-216
-
- Chapter
- Export citation
8 - Inpainting Mechanisms of Transport and Diffusion
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 174-179
-
- Chapter
- Export citation
Mordell’s equation: a classical approach
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
A quasi-linear time algorithm for computing modular polynomials in dimension 2
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 603-632
-
- Article
-
- You have access
- Export citation
Author Index
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 205-206
-
- Chapter
- Export citation
10 - Integral Representations
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 141-151
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp i-iv
-
- Chapter
- Export citation
Preface
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp vii-viii
-
- Chapter
- Export citation
Supplemental References
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 202-204
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 207-207
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 1-11
-
- Chapter
- Export citation
2 - Smoothness
-
- Book:
- Ridge Functions
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 12-18
-
- Chapter
- Export citation