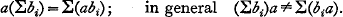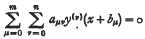Refine search
Actions for selected content:
28954 results in Differential and integral equations, dynamical systems and control theory
XLV.—The Internal and External Fields of a Particle in a Gravitational Field
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 427-433
- Print publication:
- 1949
-
- Article
- Export citation
XLII.—The Nature of Scientific Philosophy
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 400-411
- Print publication:
- 1949
-
- Article
- Export citation
L.—Quantum Theory of Rest-Masses*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 470-488
- Print publication:
- 1949
-
- Article
- Export citation
XLVII.—Non-Associative Arithmetics*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 442-453
- Print publication:
- 1949
-
- Article
- Export citation
XLVIII.—On Commuting Matrices and Commutative Algebras*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 454-459
- Print publication:
- 1949
-
- Article
- Export citation
XLIV.—The Equivalence of the Gravitational and Invariant Mass of an Isolated Body at Rest*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 424-426
- Print publication:
- 1949
-
- Article
- Export citation
XLIII.—On the Gravitational Mass of a System of Particles
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 412-423
- Print publication:
- 1949
-
- Article
- Export citation
XLIX.—Generalizations of a Problem of Pillai
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 460-469
- Print publication:
- 1949
-
- Article
- Export citation
PRM volume 62 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b8
- Print publication:
- 1949
-
- Article
-
- You have access
- Export citation
Index
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 489-491
- Print publication:
- 1949
-
- Article
- Export citation
XL.—The Linear Difference-differential Equation with Constant Coefficients
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 387-393
- Print publication:
- 1949
-
- Article
- Export citation
XLI.—Problems in Factor Analysis*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 394-399
- Print publication:
- 1949
-
- Article
- Export citation
XLVI.—The Mechanics of Continuous Matter in the Relativity Theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 434-441
- Print publication:
- 1949
-
- Article
- Export citation
PRM volume 62 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f4
- Print publication:
- 1949
-
- Article
-
- You have access
- Export citation
Corrigendum
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, p. 377
- Print publication:
- 1948
-
- Article
- Export citation
XXXVII.—The Van der Waals Force between a Proton and a Hydrogen Atom. II. Excited States
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 360-368
- Print publication:
- 1948
-
- Article
- Export citation
XXVIII.—The Discriminant of a Certain Ternary Quartic
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 268-272
- Print publication:
- 1948
-
- Article
- Export citation
Corrigendum
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, p. 277
- Print publication:
- 1948
-
- Article
- Export citation
XXXIII.—Applications of Elliptic Functions to Wind Tunnel Interference
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 316-318
- Print publication:
- 1948
-
- Article
- Export citation
XXXIX.—Transformations of Hypergeometric Functions of Two Variables
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 378-385
- Print publication:
- 1948
-
- Article
- Export citation