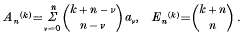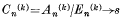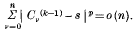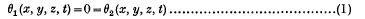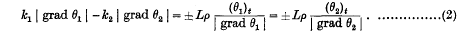Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
GMJ volume 1 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
Integrals involving E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 129-136
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
Generalisation of an Integral due to Hardy
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-117
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
III.—The Problem of Two Bodies in Whitehead's Theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 49-56
- Print publication:
- 1953
-
- Article
- Export citation
I.—On Kuiper's Theory of the Origin of the Solar System*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-8
- Print publication:
- 1953
-
- Article
- Export citation
PRM volume 64 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1953
-
- Article
-
- You have access
- Export citation
V.—Interpolatory Methods for Theorems of Vitali and Montel Type*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 71-79
- Print publication:
- 1953
-
- Article
- Export citation
VII—Tidal Charts Based on Coastal Data: Irish Sea
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 90-111
- Print publication:
- 1953
-
- Article
- Export citation
VI.—The Maximum Term of an Entire Series
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 80-89
- Print publication:
- 1953
-
- Article
- Export citation
IV.—Expansion of a Finite One-dimensional Gas Cloud into a Vacuum*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 57-70
- Print publication:
- 1953
-
- Article
- Export citation
II.—Asymptotic Renewal Theorems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 9-48
- Print publication:
- 1953
-
- Article
- Export citation
GMJ volume 1 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
Generalisations of some Integrals Involving Bessel Functions and E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 72-75
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
A Definition for Strong Rieszian Summability and its Relationship to Strong Cesaro Summability
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 94-99
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
GMJ volume 1 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
Fourier Expansions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 76-93
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
A Group-Theoretic Proof of a Theorem of MacLagan-Wedderburn
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 53-63
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
The Quadratic Law of Reciprocity and the Theory of Galois Fields
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 2 / July 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 64-71
- Print publication:
- July 1952
-
- Article
-
- You have access
- Export citation
XIX.—A Generalization of the Classical Random-walk problem, and a Simple Model of Brownian Motion Based Thereon
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 268-279
- Print publication:
- 1952
-
- Article
- Export citation
Propagation of a Boundary of Fusion
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 42-47
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
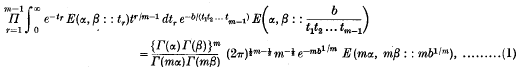
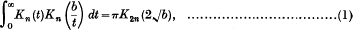
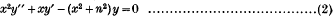
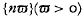 it is termed a
it is termed a 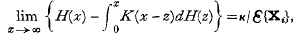
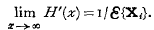
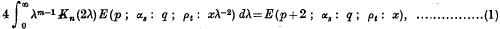
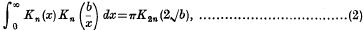
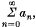 we define
we define 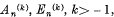 , by the relations
, by the relations