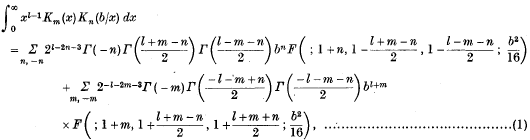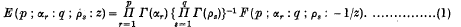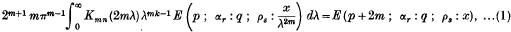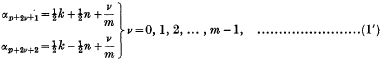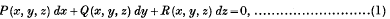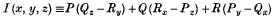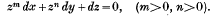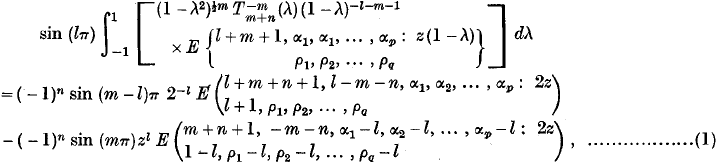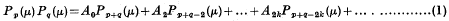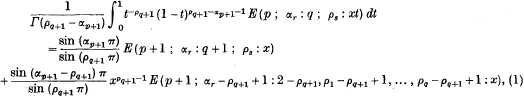Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
GMJ volume 1 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
The Schur Derivative of a Polynomial
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-163
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
A Linear Relation between E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-186
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
Integrals of E-Functions expressed in Terms of E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 192-195
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
GMJ volume 1 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
A Minimum Problem for the Epstein Zeta-Function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 149-158
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
Commutative Extension of Partial Automorphisms of Groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 170-181
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
Associated Basic Hypergeometric Series
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 182-184
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
Conduction of Heat from Local Sources in a Medium Generating or Absorbing Heat
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 164-169
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
An Infinite Integral involving a Product of Two Modified Bessel Functions of the Second Kind
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 187-189
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
Some Integrals involving E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 190-191
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
An Expression for Bernoulli Numbers
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 126-128
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
An Integral involving a Modified Bessel Function of the Second Kind and an E-function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-120
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
GMJ volume 1 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
Exceptional Integrals of a not completely Integrable Total Differential Equation
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-138
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
An Integral involving an E-function and an Associated Legendre Function of the First Kind
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 111-114
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
The Product of Two Legendre Polynomials
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-125
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
The Equivalence of Asymptotic Distributions under Randomisation and Normal Theories
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 139-147
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
On the Theory of Relaxation
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 101-110
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
Integral of an E-function expressed as a Sum of two E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 3 / September 1953
- Published online by Cambridge University Press:
- 18 May 2009, p. 118
- Print publication:
- September 1953
-
- Article
-
- You have access
- Export citation
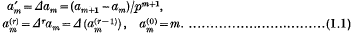
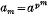 , then by Fermat's theorem
, then by Fermat's theorem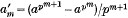
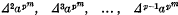
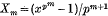 and
and 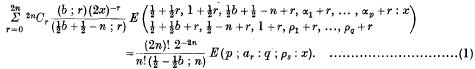
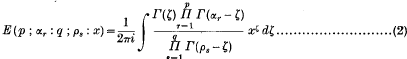
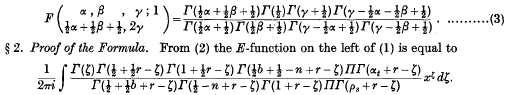
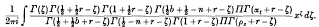
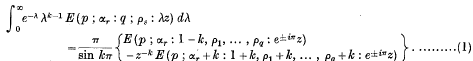
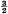 . Because of the connexion with the problems of closest packing and covering it seemed likely that the minimum value of
. Because of the connexion with the problems of closest packing and covering it seemed likely that the minimum value of