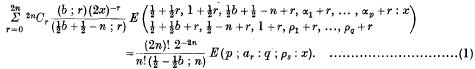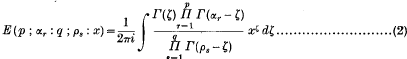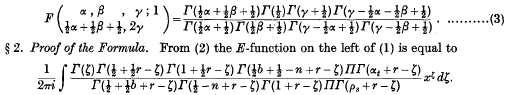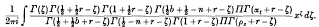Refine search
Actions for selected content:
28954 results in Differential and integral equations, dynamical systems and control theory
The Green's function of an elastic plate
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-23
- Print publication:
- June 1954
-
- Article
- Export citation
The Asymptotic Distributions of Statistics arising in Certain Non-Parametric Tests
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 1 / April 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 47-51
- Print publication:
- April 1954
-
- Article
-
- You have access
- Export citation
GMJ volume 2 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 1 / April 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- April 1954
-
- Article
-
- You have access
- Export citation
GMJ volume 2 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 1 / April 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- April 1954
-
- Article
-
- You have access
- Export citation
The Representations of Lie Algebras of Prime Characteristic
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 1 / April 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-36
- Print publication:
- April 1954
-
- Article
-
- You have access
- Export citation
Simultaneous Extension of Partial Endomorphisms of Groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 1 / April 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 37-46
- Print publication:
- April 1954
-
- Article
-
- You have access
- Export citation
Integrals Involving E-Functions and Modified Bessel Functions of the Second Kind
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 1 / April 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 52-56
- Print publication:
- April 1954
-
- Article
-
- You have access
- Export citation
XIII.—A Statistical Examination of the Centroid Method*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 175-189
- Print publication:
- 1954
-
- Article
- Export citation
XVI.—Two Hologram Methods in Diffraction Microscopy
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 209-221
- Print publication:
- 1954
-
- Article
- Export citation
X.—A Configuration of Points and Spheres in Four-dimensional Space*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 145-149
- Print publication:
- 1954
-
- Article
- Export citation
IX.—On the Geometry of Ɛ-Matrices
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 127-144
- Print publication:
- 1954
-
- Article
- Export citation
XII.—On the Theory of Unimolecular Gas Reactions: A Quantum Harmonic Oscillator Model
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 161-174
- Print publication:
- 1954
-
- Article
- Export citation
XV.—Bounds for the Indices of Nilpotent and Solvable Lie Algebras*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 200-208
- Print publication:
- 1954
-
- Article
- Export citation
PRM volume 64 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1954
-
- Article
-
- You have access
- Export citation
VIII.—Riemann Extensions which have Kähler Metrics.
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 113-126
- Print publication:
- 1954
-
- Article
- Export citation
XI.—Theory of Indices for Non-Associative Algebra*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 150-160
- Print publication:
- 1954
-
- Article
- Export citation
XIV.—Studies in Practical Mathematics. VIII. On the Iterative Methods of Lin and Friedman for Factorizing Polynomials*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 190-199
- Print publication:
- 1954
-
- Article
- Export citation
GMJ volume 1 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
The Schur Derivative of a Polynomial
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-163
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation
A Linear Relation between E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 4 / December 1953
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-186
- Print publication:
- December 1953
-
- Article
-
- You have access
- Export citation


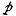 at fixed temperature,
at fixed temperature, 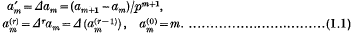
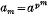 , then by Fermat's theorem
, then by Fermat's theorem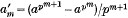
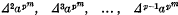
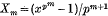 and
and