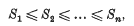Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
The representation of integers by positive ternary quadratic forms
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-110
- Print publication:
- June 1954
-
- Article
- Export citation
The triangle as a geometric variable
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 80-88
- Print publication:
- June 1954
-
- Article
- Export citation
Torsion of cylinders with inclusions*
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-103
- Print publication:
- June 1954
-
- Article
- Export citation
An Integral Involving a Product of Two Modified Bessel Functions of the Second Kind
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-88
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
Integrals Involving a Modified Bessel Function of the Second Kind and an E-Function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 93-96
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
Elliptic Integrals in Terms of Legendre Polynomials
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-99
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
A Reduction Formula
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-61
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
GMJ volume 2 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
A Problem associated with a Particular Markov Chain
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 100-104
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
GMJ volume 2 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
Further Integrals Involving E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 77-84
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
On Infinite Series of Sets
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 89-92
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
Cohomology Theory for Non-Normal Subgroups and Non-Normal Fields*
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 66-76
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
Contiguous Hypergeometric Functions of the Type 3F2(1)
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 2 / October 1954
- Published online by Cambridge University Press:
- 18 May 2009, pp. 62-65
- Print publication:
- October 1954
-
- Article
-
- You have access
- Export citation
Index to volume 1
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, p. 157
- Print publication:
- June 1954
-
- Article
- Export citation
A simple proof of η(— 1/τ)= η(τ)√τ/i
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, p. 4
- Print publication:
- June 1954
-
- Article
- Export citation
Simultaneous Diophantine Approximation
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-72
- Print publication:
- June 1954
-
- Article
- Export citation
On convergence and summability factors in a sequence
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-44
- Print publication:
- June 1954
-
- Article
- Export citation
History of Science and Psychology of Invention
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
- Print publication:
- June 1954
-
- Article
- Export citation
The minimal points of a positive definite quadratic form
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-17
- Print publication:
- June 1954
-
- Article
- Export citation
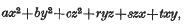
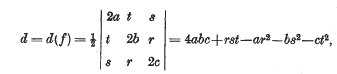
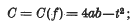
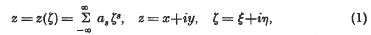

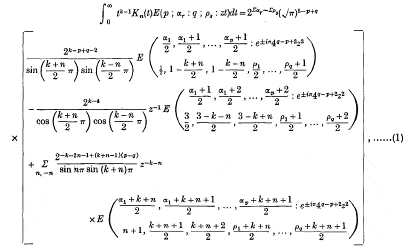
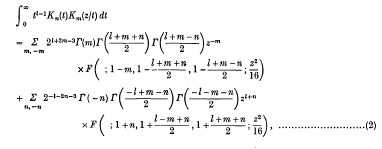
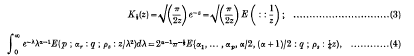
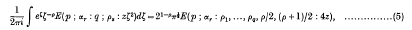



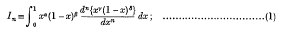

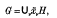
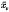
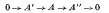
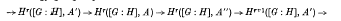
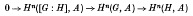





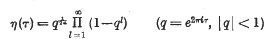
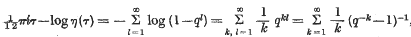
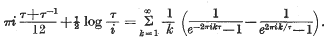
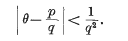

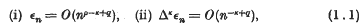
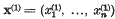 be a point at which this value is attained. Let
be a point at which this value is attained. Let