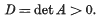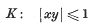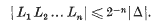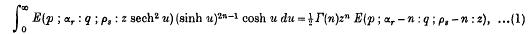Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
On the minimal points of positive definite quadratic forms
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-24
- Print publication:
- June 1956
-
- Article
- Export citation
Monotonicity of partition functions
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-14
- Print publication:
- June 1956
-
- Article
- Export citation
Note on the two-dimensional theory of anisotropic dielectrics
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-68
- Print publication:
- June 1956
-
- Article
- Export citation
Complete quadrics and collineations in Sn
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-79
- Print publication:
- June 1956
-
- Article
- Export citation
A note on Alexander's duality
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-46
- Print publication:
- June 1956
-
- Article
- Export citation
Characteristic directions of certain equations of plasticity
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-62
- Print publication:
- June 1956
-
- Article
- Export citation
A property of the star domain |xy| ≤ 1
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, p. 80
- Print publication:
- June 1956
-
- Article
- Export citation
MTK volume 3 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1956
-
- Article
-
- You have access
- Export citation
On the inhomogeneous minimum of the product of n linear forms
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-39
- Print publication:
- June 1956
-
- Article
- Export citation
The Reidemeister-Schreier and Kuroš subgroup theorems
-
- Journal:
- Mathematika / Volume 3 / Issue 1 / June 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 47-55
- Print publication:
- June 1956
-
- Article
- Export citation
Matrices Associated with Fractional Hankel and Fourier Transformations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-192
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
GMJ volume 2 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
Prime Ideals in Matrix Rings
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 193-195
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
A General Theory of One-dimensional Local Rings
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-169
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
Some Bessel Function Integrals
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 183-184
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
A Theorem in Operational Calculus and some Integrals involving Legendre, Bessel and E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-179
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
A Few Infinite Integrals involving E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 170-172
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
GMJ volume 2 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
Integrals involving Products of Bessel Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 180-182
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
A Generalization of the Inequality of the Arithmetic-Geometric Means
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 2 / Issue 4 / February 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 149-158
- Print publication:
- February 1956
-
- Article
-
- You have access
- Export citation
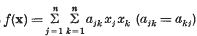 be a positive definite quadratic form in
be a positive definite quadratic form in