Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
A Note on Integer Solutions of the Diophantine Equation x2-dy2=1
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-56
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
On a result of Marshall Hall
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-110
- Print publication:
- December 1956
-
- Article
- Export citation
MTK volume 3 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
GMJ volume 3 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Note on irregularities of distribution
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-135
- Print publication:
- December 1956
-
- Article
- Export citation
Measurable almost periodic functions
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 140-143
- Print publication:
- December 1956
-
- Article
- Export citation
On a Conjecture of Hanna Neumann
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 13-17
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
On Recurrence Formulae
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 36-37
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Indefinite quadratic forms in many variables
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-101
- Print publication:
- December 1956
-
- Article
- Export citation
The Structure of Normal Inverse Semigroups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-9
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Remarks on the Upper Centralc Series of a Group
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 38-44
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Semi-regular local rings
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-126
- Print publication:
- December 1956
-
- Article
- Export citation
On Semi-Special Permutations I
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 18-35
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Thin circular plates under certain distributions of normal loading
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-152
- Print publication:
- December 1956
-
- Article
- Export citation
Extended computation of the Riemann zeta-function
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-108
- Print publication:
- December 1956
-
- Article
- Export citation
GMJ volume 3 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
On The Closed Graph Theorem
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 9-12
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Indefinite quadratic polynomials in n variables
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-116
- Print publication:
- December 1956
-
- Article
- Export citation
Index to volume 3
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, p. 164
- Print publication:
- December 1956
-
- Article
- Export citation
Covering space by spheres
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-139
- Print publication:
- December 1956
-
- Article
- Export citation
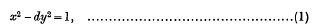
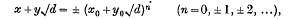
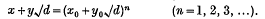
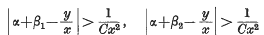
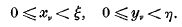
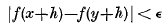
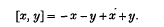
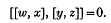
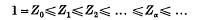
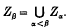 If α is the least ordinal for which
If α is the least ordinal for which 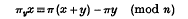
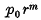 cos nϑ(or sin
cos nϑ(or sin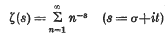
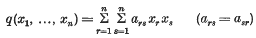
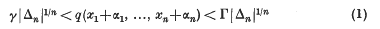
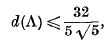
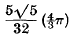 . Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.
. Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.