Refine search
Actions for selected content:
28962 results in Differential and integral equations, dynamical systems and control theory
III.—On the Moments and Regression Equations of the Fourfold Negative and Fourfold Negative Factorial Binomial Distributions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 29-34
- Print publication:
- 1958
-
- Article
- Export citation
VI.—Complex Four-dimensional Lie Algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 72-83
- Print publication:
- 1958
-
- Article
- Export citation
V.—On Certain Classes of Linear Algebras of Genus One
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 63-71
- Print publication:
- 1958
-
- Article
- Export citation
II.—On Certain Moduli of Rectangular Matrices
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 13-28
- Print publication:
- 1958
-
- Article
- Export citation
I.—On the Geometry of Metrisable Lie Algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-12
- Print publication:
- 1958
-
- Article
- Export citation
GMJ volume 3 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
Certain expansions involving E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-122
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
A note on Mathieu functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 132-134
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
The product of n linear forms in a field of series
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-137
- Print publication:
- December 1957
-
- Article
- Export citation
On the expansion of functions satisfying four boundary conditions
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 140-145
- Print publication:
- December 1957
-
- Article
- Export citation
The twisted sphere
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 162-165
- Print publication:
- December 1957
-
- Article
- Export citation
Rational approximations to algebraic numbers
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
- Print publication:
- December 1957
-
- Article
- Export citation
Cubic forms over algebraic number fields
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-101
- Print publication:
- December 1957
-
- Article
- Export citation
On a method for the determination of class number factors in number fields
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-121
- Print publication:
- December 1957
-
- Article
- Export citation
The relation between load and penetration for a spherical punch
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-161
- Print publication:
- December 1957
-
- Article
- Export citation
Index to volume 4
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, p. 169
- Print publication:
- December 1957
-
- Article
- Export citation
GMJ volume 3 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
Completely continuous movements in topological vector spaces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 135-141
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
Semigroups satisfying minimal conditions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 145-152
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
On certain relations between products of bilateral hypergeometric series
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 141-144
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
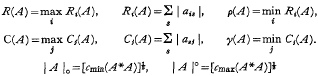
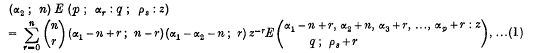
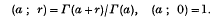

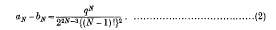
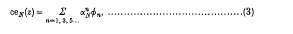
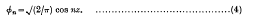
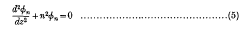

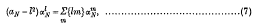
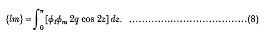
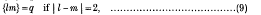
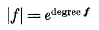
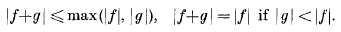
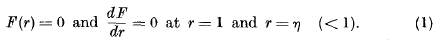

 series in terms of
series in terms of 