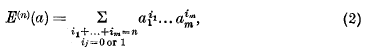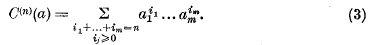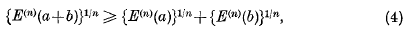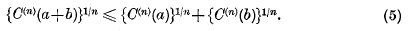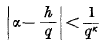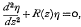Refine search
Actions for selected content:
28962 results in Differential and integral equations, dynamical systems and control theory
On rearrangements of infinite series
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 182-193
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
GMJ volume 3 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
GMJ volume 3 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
Criteria for cubic and quartic residuacity
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-29
- Print publication:
- June 1958
-
- Article
- Export citation
Derivatives of vector-valued functions
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-61
- Print publication:
- June 1958
-
- Article
- Export citation
Indefinite quadratic forms in many variables
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 8-12
- Print publication:
- June 1958
-
- Article
- Export citation
A proof of the subgroup theorem for free products
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-19
- Print publication:
- June 1958
-
- Article
- Export citation
Note on a conformal transformation
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-66
- Print publication:
- June 1958
-
- Article
- Export citation
Stress relief in a cracked plate
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-81
- Print publication:
- June 1958
-
- Article
- Export citation
On the averages of some arithmetical functions of two variables
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-7
- Print publication:
- June 1958
-
- Article
- Export citation
The separation of a viscous liquid at a straight edge
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-84
- Print publication:
- June 1958
-
- Article
- Export citation
An extension of a theorem of Heilbronn
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-37
- Print publication:
- June 1958
-
- Article
- Export citation
Some inequalities concerning symmetric forms
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-57
- Print publication:
- June 1958
-
- Article
- Export citation
The p-adic generalization of the Thue-Siegel-Roth theorem
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-48
- Print publication:
- June 1958
-
- Article
- Export citation
MTK volume 5 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1958
-
- Article
-
- You have access
- Export citation
On sequences of integers
-
- Journal:
- Mathematika / Volume 5 / Issue 1 / June 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-39
- Print publication:
- June 1958
-
- Article
- Export citation
VII.—Entropic Functions for Linear Algebras*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 84-108
- Print publication:
- 1958
-
- Article
- Export citation
PRM volume 65 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1958
-
- Article
-
- You have access
- Export citation
IV.—The Differential Equations Associated with the Uniformization of Certain Algebraic Curves*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. 35-62
- Print publication:
- 1958
-
- Article
- Export citation
PRM volume 65 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 1 / 1958
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1958
-
- Article
-
- You have access
- Export citation