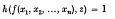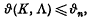Refine search
Actions for selected content:
28962 results in Differential and integral equations, dynamical systems and control theory
GMJ volume 4 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
On a problem of Rankin about the Epstein zeta-function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 73-80
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
Integration of E-functions with respect to their parameters
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 84-87
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
Dual Trigonometrical Series
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-57
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
A Note on the Angles in an n-Dimensional Simplex
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 58-61
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
Abstract theory of packings and coverings. I.
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 92-95
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
GMJ volume 4 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
Abstract theory of packings and coverings. II
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 96-100
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
On Trace Bilinear Forms on Lie-Algebras
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 62-72
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
An extension of a theorem on the equivalence between absolute Rieszian and absolute Cesàro summability
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 81-83
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
Further Duals of a verbal Subgroup
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 2 / July 1959
- Published online by Cambridge University Press:
- 18 May 2009, pp. 88-91
- Print publication:
- July 1959
-
- Article
-
- You have access
- Export citation
Note on the motion of fluid in a curved pipe
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-85
- Print publication:
- June 1959
-
- Article
-
- You have access
- Export citation
MTK volume 6 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1959
-
- Article
-
- You have access
- Export citation
Lattice coverings of space
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-39
- Print publication:
- June 1959
-
- Article
- Export citation
The stability of a column of rotating liquid
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-32
- Print publication:
- June 1959
-
- Article
- Export citation
The genus field and genus group in finite number fields
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-46
- Print publication:
- June 1959
-
- Article
- Export citation
Simple rings without zero-divisors, and Lie division rings
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-18
- Print publication:
- June 1959
-
- Article
- Export citation
Combinatorial extreme value distributions
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-76
- Print publication:
- June 1959
-
- Article
- Export citation
Products on spheres
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1959
-
- Article
- Export citation
Elastic equilibrium of completely aeolotropic cylinders: extension by longitudinal lateral loading and end forces
-
- Journal:
- Mathematika / Volume 6 / Issue 1 / June 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 47-62
- Print publication:
- June 1959
-
- Article
- Export citation
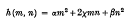
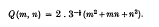
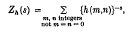
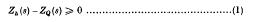
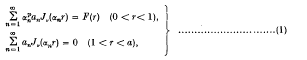
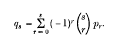

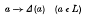

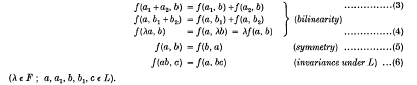
 be a given series and let
be a given series and let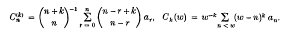
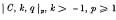 , q real, if
, q real, if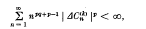
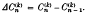 Summability |
Summability |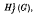 which is defined as the minimal subgroup of G containing all elements ξ of G for which
which is defined as the minimal subgroup of G containing all elements ξ of G for which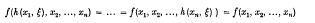
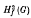 which is defined as the minimal subgroup of
which is defined as the minimal subgroup of