Refine search
Actions for selected content:
28965 results in Differential and integral equations, dynamical systems and control theory
The defect of a one-dimensional local ring
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-97
- Print publication:
- December 1959
-
- Article
- Export citation
Two centred expansion of the retarded Green's function
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-117
- Print publication:
- December 1959
-
- Article
- Export citation
Covering space with equal spheres
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-157
- Print publication:
- December 1959
-
- Article
- Export citation
On the enumerative geometry of triangles
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-164
- Print publication:
- December 1959
-
- Article
- Export citation
Rational polygons
-
- Journal:
- Mathematika / Volume 6 / Issue 2 / December 1959
- Published online by Cambridge University Press:
- 26 February 2010, p. 98
- Print publication:
- December 1959
-
- Article
- Export citation
Criteria for extreme forms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-20
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
Some extreme forms defined in terms of Abelian groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-63
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
The survival of a mutant gene under selection
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-126
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
Some nozzle flows found by the hodograph method
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 80-94
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
Application of generating functions to a problem in finite dam theory*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 116-120
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
Recurrence of extreme observations*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 106-112
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
JAZ volume 1 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
The generation by two operators of the symplectic group over GF(2)*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 38-46
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
On the strength of sand
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 71-79
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
Measurability of functions of two variables
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-26
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
A note on the finite Fourier transform
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-98
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
On Euler's criterion
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-70
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
Discontinuous solutions of variational problems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-37
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
On the trace of the energy-momentum tensor of fields associated with particles of zero rest mass
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 99-105
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
On distributions whose moments are majorated by the moments of a known distribution*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-115
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation
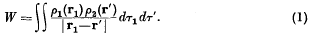
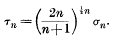
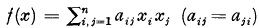 , of determinant
, of determinant 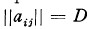 and minimum M for integral
and minimum M for integral 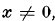 , is said to be extreme if the ratio
, is said to be extreme if the ratio 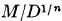 is a (local) maximum for small variations in the coefficients
is a (local) maximum for small variations in the coefficients 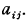 .
.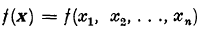 be a positive definite quadratic form of determinant
be a positive definite quadratic form of determinant 

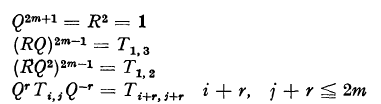
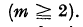 .
.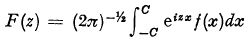
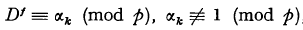
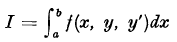
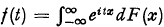 its characteristic function and by
its characteristic function and by 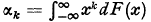 its moment of order
its moment of order 

