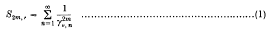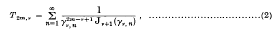Refine search
Actions for selected content:
28969 results in Differential and integral equations, dynamical systems and control theory
Symmetrically loaded shallow shells of revolution
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-35
- Print publication:
- June 1960
-
- Article
- Export citation
On infinitesimal triangles
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-14
- Print publication:
- June 1960
-
- Article
- Export citation
Über die Normalstruktur von mehrfach faktorisierten Gruppen
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-146
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
Continuously infinite matrices and the algebraic theory of Fredholm's equation
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
On random interpolation
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-133
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
On the spaces of certain classes of entire functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 147-170
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
On the theory of a cascade of stalled aerofoils
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 210-219
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
Some entire functions with fixpoints of every order
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 203-209
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
Unsteady flow through a cascade of aerofoils
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 220-232
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
Quadratic forms in Poisson and multi-nomial variables
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-240
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
JAZ volume 1 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
Roger Chapman Thorne
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 255-256
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
An n-dimensional analogue of Cauchy's integral theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-202
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
JAZ volume 1 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
On Tests of independence in several dimensions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 2 / February 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-254
- Print publication:
- February 1960
-
- Article
-
- You have access
- Export citation
XIII.—A Remark on Coefficients in Certain Asymptotic Expansions*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 3 / 1960
- Published online by Cambridge University Press:
- 14 February 2012, pp. 205-206
- Print publication:
- 1960
-
- Article
- Export citation
GMJ volume 4 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 3 / January 1960
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1960
-
- Article
-
- You have access
- Export citation
XVI.—The Synthesis of 1, 6-Naphthyridine*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 3 / 1960
- Published online by Cambridge University Press:
- 14 February 2012, pp. 231-236
- Print publication:
- 1960
-
- Article
- Export citation
XVII.—Inherited Measures*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 3 / 1960
- Published online by Cambridge University Press:
- 14 February 2012, pp. 237-246
- Print publication:
- 1960
-
- Article
- Export citation
On some infinite series involving the zeros of Bessel functions of the first kind
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 3 / January 1960
- Published online by Cambridge University Press:
- 18 May 2009, pp. 144-156
- Print publication:
- January 1960
-
- Article
-
- You have access
- Export citation




 represent the deviations from expectation of a set of multinomial or independent Poisson variables, and Η be a positive definite matrix. A lower bound is obtained for
represent the deviations from expectation of a set of multinomial or independent Poisson variables, and Η be a positive definite matrix. A lower bound is obtained for  in terms of
in terms of  , Where
, Where  is a vector of normal variables with the same mean and covariance matrix as Δ.
is a vector of normal variables with the same mean and covariance matrix as Δ.