Refine search
Actions for selected content:
28969 results in Differential and integral equations, dynamical systems and control theory
XXII.—Some Nilpotent Algebras with Centres of Given Dimension
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 310-317
- Print publication:
- 1961
-
- Article
- Export citation
PRM volume 65 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1961
-
- Article
-
- You have access
- Export citation
The Divisors of a Quadratic Polynomial
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 8-20
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
Index
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 381-383
- Print publication:
- 1961
-
- Article
- Export citation
Asymptotic formulae for solutions of linear second-order differential equations with a large parameter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 439-464
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
The expansion of functions in ultraspherical polynomials
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 428-438
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
Indefinite quadratic polynomials
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-144
- Print publication:
- December 1960
-
- Article
- Export citation
JAZ volume 1 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
Green's functions for thin perforated elastic slabs
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-112
- Print publication:
- December 1960
-
- Article
- Export citation
The survival of a mutant gene under selection. II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 485-491
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
Certain subgroups of free products
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-124
- Print publication:
- December 1960
-
- Article
- Export citation
Some elastic and thermoelastic stress distributions in a semi-infinite solid
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-160
- Print publication:
- December 1960
-
- Article
- Export citation
Expectation values of operators in the quasi chemical equilibrium theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 465-484
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
On statistical independence and zero correlation in several dimensions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 492-496
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
JAZ volume 1 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f3
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
The existence of parametric surface integrals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 4 / December 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-427
- Print publication:
- December 1960
-
- Article
-
- You have access
- Export citation
On a theorem of P. J. Cohen
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-97
- Print publication:
- December 1960
-
- Article
- Export citation
On a theorem of Mahler
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-140
- Print publication:
- December 1960
-
- Article
- Export citation
An application of Jensen's formula to polynomials
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-100
- Print publication:
- December 1960
-
- Article
- Export citation
Index to volume 7
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, p. 172
- Print publication:
- December 1960
-
- Article
- Export citation
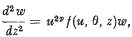
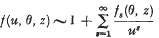
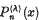 (
(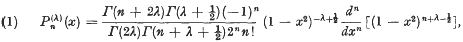
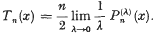
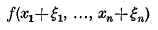
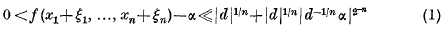
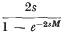
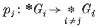 may be defined by requiring it to be trivial on
may be defined by requiring it to be trivial on