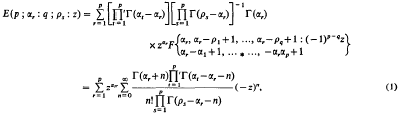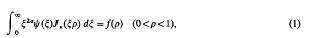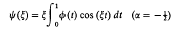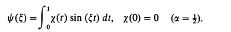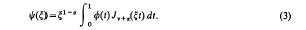Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
JAZ volume 2 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
Lattice embeddings of prime power groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-34
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
JAZ volume 2 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
On a problem of G. Golomb.
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-8
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
Pulse diffraction by an imperfectly reflecting wedge
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-106
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
On the differential equations of H. Lewy
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-16
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
The Divisibility of Divisor Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 35-40
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
Note on a conjecture of Coxeter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 25-29
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
XXV.—Properties of I-extensions of Anti-commutative Algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 345-357
- Print publication:
- 1961
-
- Article
- Export citation
A Structure Theorem for Topological Lattices
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-3
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
XXVIII.—The Synthesis of 7-Substituted Fluoranthenes*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 376-380
- Print publication:
- 1961
-
- Article
- Export citation
A Basic Analogue of MacRobert's E-Function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 4-7
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
GMJ volume 5 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
XXI—The Evaluation of a Definite Integral Which Occurs in Asymptotic Partition Theory*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 283-309
- Print publication:
- 1961
-
- Article
- Export citation
XXIII.—Representations of a Number as the Sum of a Large Number of Squares*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 318-331
- Print publication:
- 1961
-
- Article
- Export citation
Evaluation of an E-Function when two of the upper Parameters differ by an Integer
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 30-34
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
XXIV.—Sets of Integers Containing not more than a Given Number of Terms in Arithmetical Progression*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. 332-344
- Print publication:
- 1961
-
- Article
- Export citation
GMJ volume 5 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f10
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
On Certain Dual Integral Equations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 1 / January 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-24
- Print publication:
- January 1961
-
- Article
-
- You have access
- Export citation
PRM volume 65 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 65 / Issue 4 / 1961
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1961
-
- Article
-
- You have access
- Export citation

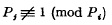
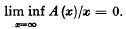
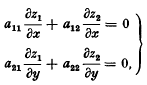
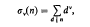
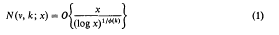
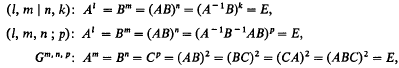
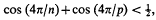
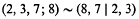
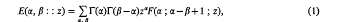
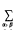 denotes that to the expression following it, a similar expression with α and β interchanged is to be added. For (1) he also gave the integral representation
denotes that to the expression following it, a similar expression with α and β interchanged is to be added. For (1) he also gave the integral representation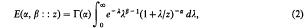
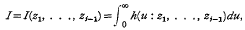
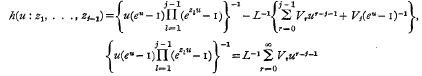
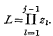 Asymptotic expansions are obtained for
Asymptotic expansions are obtained for