Refine search
Actions for selected content:
28970 results in Differential and integral equations, dynamical systems and control theory
Tests for discriminant functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-252
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
Note on the harmonic oscillator in general relativity
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 206-208
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
Evaluation of determinant of 11th order in the theory of partitions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 151-152
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
On the busy period in the queueing system GI/G/1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-228
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
The order cycle system Of stock control
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-216
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
On dominated convergence
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-136
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
A property of an iteration process
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-194
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
Dense scales of functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-142
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
On paracompact regular spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 147-150
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
The general theory of canonical correlation and its relation to functional analysis
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-242
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
A theoretical investigation of an aerofoil equipped with a split flap
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 2 / October 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 195-205
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
On a Theorem of Hurwitz
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 90-96
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
The product of two ultraspherical polynomials
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 76-79
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
GMJ volume 5 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b6
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
A Note on Regular Coverings of Closed Orientable Surfaces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-66
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
Factorization of Matrices and Minkowski's Conjecture
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 86-89
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
Invariant Measures on Coset Spaces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 80-85
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
GMJ volume 5 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
Arithmetical Functions of a Greatest Common Divisor, III. Cesàro's Divisor Problem
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 67-75
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
On the non-specialisation of intersections on a singular variety
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-44
- Print publication:
- June 1961
-
- Article
- Export citation
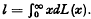 . The quantity l
. The quantity l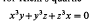
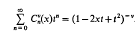
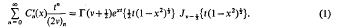
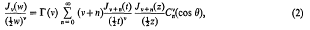
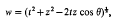
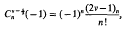
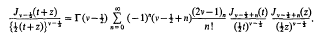
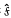 and f be the fundamental groups respectively. Then
and f be the fundamental groups respectively. Then 
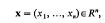
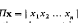 , and (as usual)
, and (as usual) 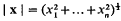 so that, by the inequality of arithmetic and geometric means,
so that, by the inequality of arithmetic and geometric means,

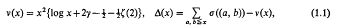
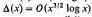 . This estimate was later improved to
. This estimate was later improved to 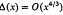 . The precise statement of the result for σ((
. The precise statement of the result for σ((