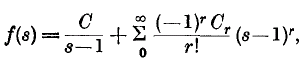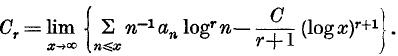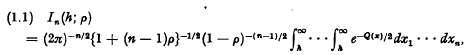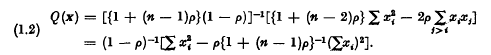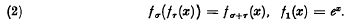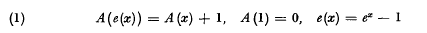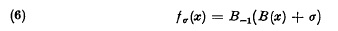Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
The addition of norm forms
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-82
- Print publication:
- June 1962
-
- Article
- Export citation
On some axisymmetrical two sphere potential problems
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-70
- Print publication:
- June 1962
-
- Article
- Export citation
An extension of a theorem of König on graphs
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 9-10
- Print publication:
- June 1962
-
- Article
- Export citation
Continued fractions of transcendental numbers
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-8
- Print publication:
- June 1962
-
- Article
- Export citation
MTK volume 9 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, p. f1
- Print publication:
- June 1962
-
- Article
-
- You have access
- Export citation
Some axially symmetric stress distributions in elastic solids containing penny-shaped cracks. II. Cracks in solids under torsion
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-37
- Print publication:
- June 1962
-
- Article
- Export citation
A slow fluid motion between two spheres
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-87
- Print publication:
- June 1962
-
- Article
- Export citation
Some Abelian results for Dirichlet series
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-53
- Print publication:
- June 1962
-
- Article
- Export citation
The group of rotations in a plane over GF(2n)
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-74
- Print publication:
- June 1962
-
- Article
- Export citation
On the Clifford collineation, transform and similarity groups. (III) Generators and involutions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-344
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
JAZ volume 2 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
The use of Spitzer's identity in the investigation of the busy period and other quantities in the queue GI/G/1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-356
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
An asymptotic expansion for a class of multivariate normal integrals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-264
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
Fractional iteration of exponentially growing functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-320
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
On sequences of integrable functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-300
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
JAZ volume 2 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
Tables of the logaritm of iteration of ex—1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-333
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
On certain identities involving basic spinors and curvature spinors
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-379
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
The practical use of variation principles in non-linear mechanics
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-368
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
Permutable power series and regular iteration
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 265-294
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
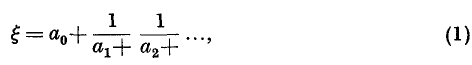

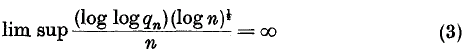
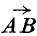 .
.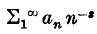 and if
and if 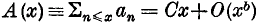 where 0 ≤
where 0 ≤