Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
GMJ volume 6 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
Inverses of Boolean matrices
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-53
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
Note on the basic assumptions of elastic plate theories
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-132
- Print publication:
- December 1962
-
- Article
- Export citation
Monoidal transformations in a one-dimensional local ring
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-144
- Print publication:
- December 1962
-
- Article
- Export citation
An approximate stochastic model for phage reproduction in a bacterium
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 478-483
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
MTK volume 9 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, p. f1
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
Sets non-σ-finite for Hausdorff measures
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 95-103
- Print publication:
- December 1962
-
- Article
- Export citation
Expectation values of operators in the quasi-chemical equilibrium theory part II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 464-477
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
On circuits and subgraphs of chromatic graphs
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-175
- Print publication:
- December 1962
-
- Article
- Export citation
Index to volume 9
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, p. 176
- Print publication:
- December 1962
-
- Article
- Export citation
Approximation properties of measures generated by continuous set functions
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-156
- Print publication:
- December 1962
-
- Article
- Export citation
A result relating to the local uniformisation theorem
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-110
- Print publication:
- December 1962
-
- Article
- Export citation
JAZ volume 2 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
The stability of an incompressible jet with an aligned magnetic field
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 162-169
- Print publication:
- December 1962
-
- Article
- Export citation
A continuous-time treatment of certain queues and infinite dams
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 484-498
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
Single server queues with modified service mechanisms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 499-507
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
An expansion method for singular perturbation problems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 440-463
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
On the genus of curves over finite fields
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-117
- Print publication:
- December 1962
-
- Article
- Export citation
On non-ramified extensions with prescribed Galois group
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-134
- Print publication:
- December 1962
-
- Article
- Export citation
Symmetrisable operators*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 381-402
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
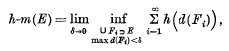
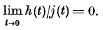
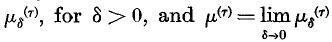 (see §3). When, for every
(see §3). When, for every 