Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
JAZ volume 2 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
A transcendence measure for E-functions
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-161
- Print publication:
- December 1962
-
- Article
- Export citation
On a nonlinear boundary value problem involving a small parameter*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-439
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
A note on the Hilbert functions of certain ideals which are defined by matrices
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-126
- Print publication:
- December 1962
-
- Article
- Export citation
Altitudes of a simplex in n-space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 4 / December 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-424
- Print publication:
- December 1962
-
- Article
-
- You have access
- Export citation
Average distances between points in a square
-
- Journal:
- Mathematika / Volume 9 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-114
- Print publication:
- December 1962
-
- Article
- Export citation
Group algebras with radicals of square zero
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 158-159
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
On Riesz summability factors
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 188-196
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
GMJ volume 5 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
Upon A Second Confluent Form of the Ɛ-Algorithm†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 160-165
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
An identity in combinatorial analysis
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 197-200
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
Some infinite integrals involving E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 183-187
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
Some definitions of Klein's simple group of order 168 and other groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 166-175
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
GMJ volume 5 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
A characterization of inaccessible cardinals
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-157
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
Torsion of beams of L-cross-section
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 4 / July 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 176-182
- Print publication:
- July 1962
-
- Article
-
- You have access
- Export citation
Reversion of a formal power series
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-94
- Print publication:
- June 1962
-
- Article
- Export citation
Thermal damping of a vibrating elastic body
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-48
- Print publication:
- June 1962
-
- Article
- Export citation
A moment theory of elastic plates
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 11-24
- Print publication:
- June 1962
-
- Article
- Export citation
Two special cubic surfaces
-
- Journal:
- Mathematika / Volume 9 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-56
- Print publication:
- June 1962
-
- Article
- Export citation
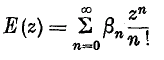
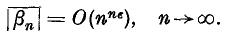


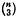 of them, thus indicating the associated character of the altitudes as discussed separately in 2 other papers (12; 16). Before we introduce an orthogonal simplex and develop its properties in regard to its γ-altitudes and associated hyperspheres, we come across a number of intermediate ones of special interest. Two special types are treated here and the other two are developed in 2 other papers (13; 15).
of them, thus indicating the associated character of the altitudes as discussed separately in 2 other papers (12; 16). Before we introduce an orthogonal simplex and develop its properties in regard to its γ-altitudes and associated hyperspheres, we come across a number of intermediate ones of special interest. Two special types are treated here and the other two are developed in 2 other papers (13; 15).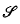 of
of 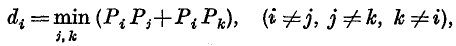

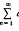 and a number
and a number