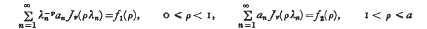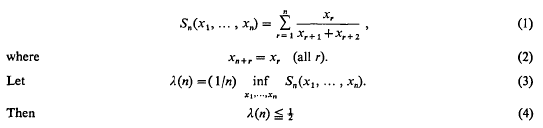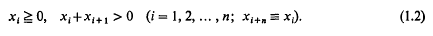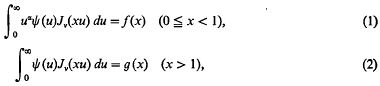Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
XIII.—Layered Systems Subjected to Asymmetric Surface Shears*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 140-149
- Print publication:
- 1963
-
- Article
- Export citation
Extension of partial endomorphisms of abelian groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 45-48
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
GMJ volume 6 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
An embedding theorem with amalgamation for cancellative semigroups†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 19-26
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
On harmonic continuation
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 54-56
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
XVII.—Dual Series Relations. IV. Dual Relations Involving Series of Jacobi Polynomials
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 185-191
- Print publication:
- 1963
-
- Article
- Export citation
Positive matrices and eigenvectors†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 27-30
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
The solution of a pair of dual integral equations†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 14-18
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
XV.—Dual Series Relations* II. Dual Relations Involving Dini Series
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 161-172
- Print publication:
- 1963
-
- Article
- Export citation
XVI.—Dual Series Relations. III. Dual Relations Involving Trigonometric Series
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 173-184
- Print publication:
- 1963
-
- Article
- Export citation
XII.—Paraboloidal Co-ordinates and Laplace's Equation*†
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 129-139
- Print publication:
- 1963
-
- Article
- Export citation
Integrals involving E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 31-33
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
PRM volume 66 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1963
-
- Article
-
- You have access
- Export citation
Some further properties of a q-analogue of MacRobert's E-function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 34-38
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
XIV.—Dual Series Relations. I. Dual Relations Involving Fourier-Bessel Series*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 150-160
- Print publication:
- 1963
-
- Article
- Export citation
PRM volume 66 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1963
-
- Article
-
- You have access
- Export citation
XVIII.—The Emission of Long-Range Alpha Particles in Fission
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 3 / 1963
- Published online by Cambridge University Press:
- 14 February 2012, pp. 192-209
- Print publication:
- 1963
-
- Article
- Export citation
On a cyclic sum
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 11-13
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
Sur une inégalité
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-10
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
On the solution of certain dual integral equations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 1 / January 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-44
- Print publication:
- January 1963
-
- Article
-
- You have access
- Export citation
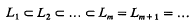
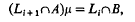
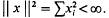 . The least such constant
. The least such constant 
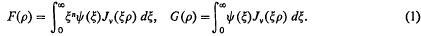
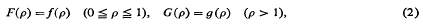
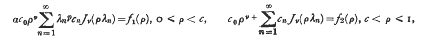
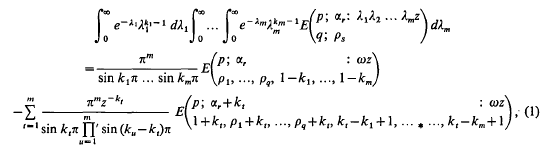
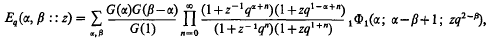
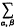 denotes that a similar expression with a and β interchanged is to be added to the expression following it. It has since then been generalized by N. Agarwal [2], who defined and studied the
denotes that a similar expression with a and β interchanged is to be added to the expression following it. It has since then been generalized by N. Agarwal [2], who defined and studied the