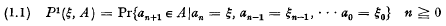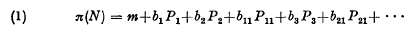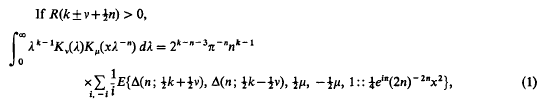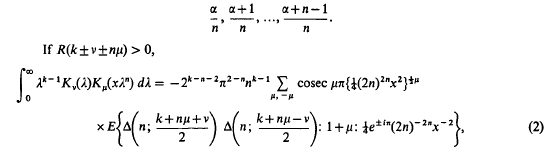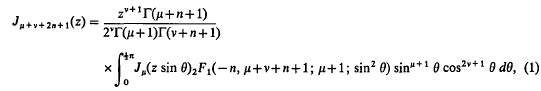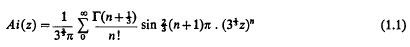Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
A limit theorem for Markov chains with continuous state space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-358
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Hilbert spaces of generalized functions extending L2, (II)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 267-281
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
The mean time for absorption in a process of genetic type
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 375-383
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
A perturbation approach to Bose-condensed pairs
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-324
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
The calculation of π(N)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-266
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Diffraction of plane elastic waves by a crack, with application to a problem of brittle fracture
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-339
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Infinite non-linear programming
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 294-300
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Diploid populations with selection depending on gene frequency
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 359-374
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
The ℋ-equivalence in a compact semigroup II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 288-293
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Arithmetics in Cayley's algebra
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-106
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
Corrigendum
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, p. 116
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
GMJ volume 6 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
A generalisation of Divinsky's radical
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 75-87
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
GMJ volume 6 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f3
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
A polynomial iteration for the spectral family of an operator
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 65-69
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
An arithmetic characterization of the parabolic points of G(2cos π/5)
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 88-96
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
Thomas Murray MacRobert
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-64
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
Integrals involving products of modified Bessel functions of the second kind
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 70-74
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
A generalization of Sonine's first finite integral
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-98
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation
On the asymptotic expansion of Airy's Integral
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 2 / July 1963
- Published online by Cambridge University Press:
- 18 May 2009, pp. 113-115
- Print publication:
- July 1963
-
- Article
-
- You have access
- Export citation