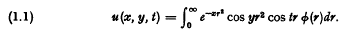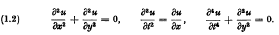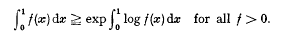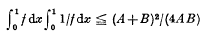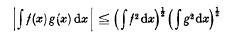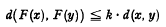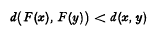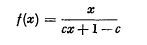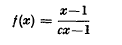Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Preemptive priority queues
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 491-502
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
On the approximation of algebraic numbers by algebraic integers
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 408-434
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
A theorem on partitions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 435-441
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
Upper and Lower bounds for a certain class of constrained variational problems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-453
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
On partial sums of Lagrange's series with application to the theory of queues
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 488-490
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
Asymptotic transient behaviour of the bulk service queue
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 503-512
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
On H. Simpson's six-conic theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 454-455
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
Functions of three variables which satisfy both the heat equation and Laplace's equation in two variables
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 396-407
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
Zumino's theorem in the quasi-chemical equilibrium theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 456-467
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
Some general results on random walks, with genetic applications
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 468-479
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
On continuous time models in the theory of dams
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 480-487
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
On a class of inequalities
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 442-448
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
A fixed point theorem with applications to convolution equations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 4 / November 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-395
- Print publication:
- November 1963
-
- Article
-
- You have access
- Export citation
Monogenic normal systems are universal1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-306
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Initial value problems in water wave theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 340-350
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation
Monotone functions mapping the set of rational numbers on itself
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 3 / August 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 282-287
- Print publication:
- August 1963
-
- Article
-
- You have access
- Export citation