Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
The limit theorem for aperiodic discrete renewal processes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 122-128
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
Symmetrisable operators :Part III Hilbert space operators Symmetrisable by bounded operators
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 31-48
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
Symmetrisable operators: Part II Operators in a Hilbert Space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-30
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
The double-six of lines over PG (3, 4)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-89
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
On perfect and extreme forms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-77
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
JAZ volume 4 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
Categories of certain minimal topological spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-82
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
On a convergence test of Hardy-Littlewood's type for fourier series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 49-55
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
On finite groups whose 2-Sylow subgroups have cyclic subgroups of index 2*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-112
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
On projective-symmetric spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-121
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
XXI.—A New Approach to the Statistical Thermodynamics of Liquids
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. 232-251
- Print publication:
- 1964
-
- Article
- Export citation
On Gordon's method of solving dual integral equations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 117-122
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
PRM volume 66 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1964
-
- Article
-
- You have access
- Export citation
On generating points of a lattice in the region
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 141-155
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
XX.—Differential Geometry on Hypersurfaces in a Cayley Space
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. 216-231
- Print publication:
- 1964
-
- Article
- Export citation
PRM volume 66 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b6
- Print publication:
- 1964
-
- Article
-
- You have access
- Export citation
XXII.—The Ullmann Synthesis of 3-Bromofluorenone*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. 252-257
- Print publication:
- 1964
-
- Article
- Export citation
GMJ volume 6 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
An improved method for dual trigonometrical series
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 136-140
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
The solution of dual series and dual integral equations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-129
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
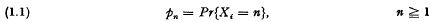
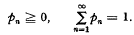
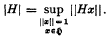
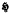
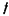 (х) =
(х) = 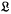 is the lattice of topologies on a set
is the lattice of topologies on a set  is a Hausdorff (or regular, or completely regular, or normal, or locally compact) topology does there always exist a minimal Hausdorff (or minimal regular, or minimal completely regular, or minimal normal, or minimal locally compact) topology weaker than
is a Hausdorff (or regular, or completely regular, or normal, or locally compact) topology does there always exist a minimal Hausdorff (or minimal regular, or minimal completely regular, or minimal normal, or minimal locally compact) topology weaker than 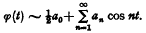
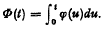
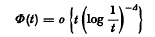
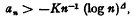
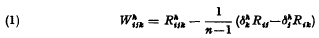



 , the sign being chosen to ensure that Δ
, the sign being chosen to ensure that Δ
