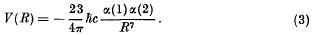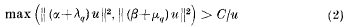Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Perfect difference sets
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 177-184
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Some inclusion theorems
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 161-168
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
GMJ volume 6 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Notes on two lemmas concerning the Epstein zeta-function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 202-204
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Another proof of the theorems on the eigenvalues of a square quaternion matrix
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 191-195
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
On polylogarithms
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 169-171
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Note on a paper of Tsuzuku
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 196-197
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Series involving products of two E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 172-176
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Extreme points of convex sets without completeness of the Scalar field
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 59-63
- Print publication:
- June 1964
-
- Article
- Export citation
On the Torsional impulsive body force within an elastic half space
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-82
- Print publication:
- June 1964
-
- Article
- Export citation
Approximation problems for convex polyhedra
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 9-18
- Print publication:
- June 1964
-
- Article
- Export citation
MTK volume 11 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1964
-
- Article
-
- You have access
- Export citation
A Slow motion of viscous liquid caused by a slowly moving solid sphere
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-74
- Print publication:
- June 1964
-
- Article
-
- You have access
- Export citation
Wave propagation in rotating elastic media
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-38
- Print publication:
- June 1964
-
- Article
- Export citation
A Correction
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-90
- Print publication:
- June 1964
-
- Article
-
- You have access
- Export citation
Analytic sets in Hausdorff spaces
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-8
- Print publication:
- June 1964
-
- Article
- Export citation
On the Interaction between two identical neutral dipole systems, One in an excited state and the other in the ground state
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-94
- Print publication:
- June 1964
-
- Article
- Export citation
A remark on relative integral bases for infinite extensions of finite number fields
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-66
- Print publication:
- June 1964
-
- Article
- Export citation
The Trigonometry of GF(22n) and Finite Hyperbolic Planes
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-88
- Print publication:
- June 1964
-
- Article
- Export citation
A note on Diophantine approximation (II)
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-58
- Print publication:
- June 1964
-
- Article
- Export citation
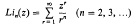
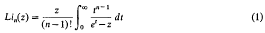

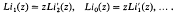
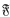 . The real number field will be denoted by
. The real number field will be denoted by 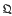 . Many of the basic notions in the theory of convexity (convex set, extreme point, hyperplane, etc.) can be defined in the general case just as they are when
. Many of the basic notions in the theory of convexity (convex set, extreme point, hyperplane, etc.) can be defined in the general case just as they are when 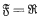 , but their behaviour may be different from that in the real case. By way of example, we consider the following theorem (due essentially to Minkowski), which is of fundamental importance both for geometric investigations and for the applications of convexity in analysis:
, but their behaviour may be different from that in the real case. By way of example, we consider the following theorem (due essentially to Minkowski), which is of fundamental importance both for geometric investigations and for the applications of convexity in analysis: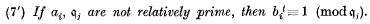
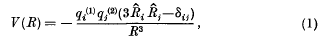
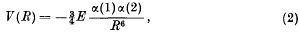
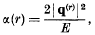
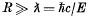 was given by Casimir and Polder as
was given by Casimir and Polder as