Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Laminar wall-jet mixing of two different gases
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-28
- Print publication:
- June 1964
-
- Article
- Export citation
On the distribution of the roots of polynomial congruences
-
- Journal:
- Mathematika / Volume 11 / Issue 1 / June 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-49
- Print publication:
- June 1964
-
- Article
- Export citation
JAZ volume 4 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
On the characteristic functional for a replacement model
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-243
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Recurrence properties of Processes with stationary independent increments
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-228
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Fractional iteration near a fixpoint of multiplier 1.
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-148
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Twisted group algebras and their representations
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 152-173
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Fractional iteration of entire and rational functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-142
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
On a theorem of Halmos concerning unbiased estimation of moments
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-232
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Felix Adalbert Behrend
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 264-270
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
On linear p-groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 174-178
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Integration of real-valued set functions in abstract Spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 202-213
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Note on Schröder's functional equation
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-151
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
On Runge-Kutta processes of high order
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-194
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
A lemma on maximal sets and the theorem of Denjoy-Vitali
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 195-201
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Imbedded Markov chain analysis of single server bulk queues
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 244-263
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
Two probability theorems and their application to some first passage problems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-222
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
JAZ volume 4 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 2 / May 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- May 1964
-
- Article
-
- You have access
- Export citation
JAZ volume 4 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
The inversion of a transform related to the Laplace transform and to heat conduction*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 1 / February 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-14
- Print publication:
- February 1964
-
- Article
-
- You have access
- Export citation
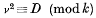
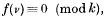
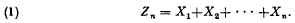
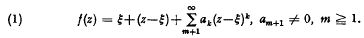
 be a finite group,
be a finite group, 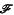 a field. A
a field. A 

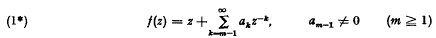
 be a class of distribution functions over a given (Borel) subset
be a class of distribution functions over a given (Borel) subset  an abstract space of points
an abstract space of points