Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
XXIII.— Dual Series Relations.* V. A Generalized Schlömilch Series and the Uniqueness of the Solution of Dual Equations involving Trigonometric Series
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. 258-268
- Print publication:
- 1964
-
- Article
- Export citation
A note on the associated Legendre polynomials
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 156-160
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
GMJ volume 6 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
Index
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. 269-271
- Print publication:
- 1964
-
- Article
- Export citation
Integrals involving products of Bessel functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 130-132
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
A note on principal sequences
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 3 / January 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 133-135
- Print publication:
- January 1964
-
- Article
-
- You have access
- Export citation
XIX.—The Cayley-Hamilton Theorem for Semi-rings*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 4 / 1964
- Published online by Cambridge University Press:
- 14 February 2012, pp. 211-215
- Print publication:
- 1964
-
- Article
- Export citation
MTK volume 10 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1963
-
- Article
-
- You have access
- Export citation
Sums of m-th powers in p-adic rings
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-146
- Print publication:
- December 1963
-
- Article
- Export citation
A problem of Dade on quadratic forms
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-106
- Print publication:
- December 1963
-
- Article
- Export citation
An elementary derivation of certain homological inequalities
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 114-124
- Print publication:
- December 1963
-
- Article
- Export citation
Coprime mappings between sets of consecutive integers
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-136
- Print publication:
- December 1963
-
- Article
- Export citation
Decomposable convex polyhedra
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-95
- Print publication:
- December 1963
-
- Article
- Export citation
Index to volume 10
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, p. 165
- Print publication:
- December 1963
-
- Article
- Export citation
A note on cracks under longitudinal shear
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-113
- Print publication:
- December 1963
-
- Article
- Export citation
Index to Volume 1–10 1954–1963
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-182
- Print publication:
- December 1963
-
- Article
- Export citation
A Stokes flow problem between two non-concentric cylinders
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-156
- Print publication:
- December 1963
-
- Article
- Export citation
Covering a sphere with spheres
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 157-164
- Print publication:
- December 1963
-
- Article
- Export citation
Algebraic integral representations by arbitrary forms
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-100
- Print publication:
- December 1963
-
- Article
- Export citation
Rational polygons
-
- Journal:
- Mathematika / Volume 10 / Issue 2 / December 1963
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
- Print publication:
- December 1963
-
- Article
- Export citation
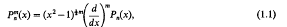
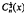 and using [3, p. 176]
and using [3, p. 176]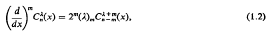
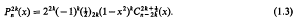
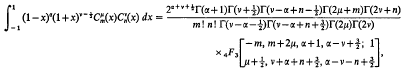
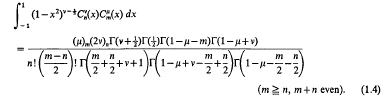
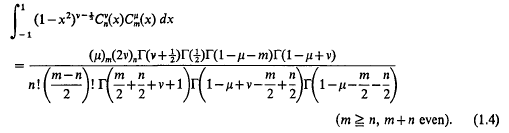
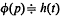 will be used to denote the classical Laplace integral relation
will be used to denote the classical Laplace integral relation

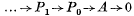
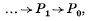
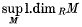 is called the
is called the 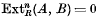 for all left
for all left 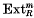 regarded as a functor of left
regarded as a functor of left