Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
JAZ volume 4 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
An integral equation from phytology
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-402
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
The joint distribution of occupation totals for a simple random walk
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 518-528
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
JAZ volume 4 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
JAZ volume 4 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Stochastic non-linear programming
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-353
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Projectivities in finite groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-326
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Comments on the preceding paper of Michael's
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-288
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Asymptotic properties of least-squares estimates of parameters of the spectrum of a stationary non-deterministic time-series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-384
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
On the radical of a category
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-307
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Right invariant integrals on locally compact semigroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-286
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Averaging operators on the ring of continuous functions on a compact space1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 293-298
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
A note on Green's Theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-292
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Computation of the generalised factorial function
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 342-346
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
Doppler broadened contour functions in the complex domain
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-362
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
JAZ volume 4 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
A generalization of z!
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 3 / August 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-341
- Print publication:
- August 1964
-
- Article
-
- You have access
- Export citation
A lemma about the Epstein zeta-function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 198-201
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
Residuation theory and Boolean matrices
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-190
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
GMJ volume 6 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 6 / Issue 4 / July 1964
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1964
-
- Article
-
- You have access
- Export citation
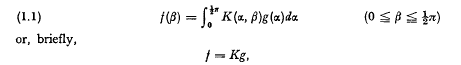
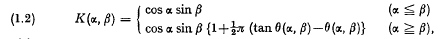
 (G) of subnormal subgroups of group G have been considered by various authors, see for example Barnes [1] and Tamaschke [2].
(G) of subnormal subgroups of group G have been considered by various authors, see for example Barnes [1] and Tamaschke [2].
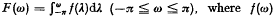 is the spectral density function. It is well known that {x
is the spectral density function. It is well known that {x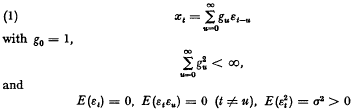
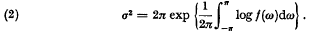
 and
and  and an additive functor
and an additive functor 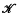 of
of 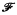 of continuous real-valued functions on ς with compact supports. If ς has the property: (A) for each pair of compact sets
of continuous real-valued functions on ς with compact supports. If ς has the property: (A) for each pair of compact sets 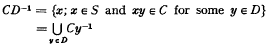
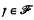 and a ∈ S, the function
and a ∈ S, the function 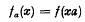
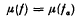
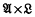 such that
such that 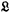 supports a measure
supports a measure 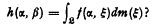
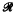 (z) < 0, (z: k)! is analytic in both variables, and that F(z) may be expressed in the form F(z) = πz/(z: k)!(—z: k)!
(z) < 0, (z: k)! is analytic in both variables, and that F(z) may be expressed in the form F(z) = πz/(z: k)!(—z: k)!