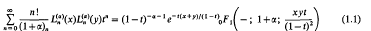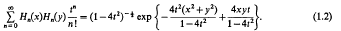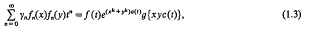Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Some asymptotic results for the periodogram of a stationary time series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 107-128
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 1 Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
VIII.—An Objective Criterion of the Limit of Useful Sophistication of the Semi-empirical Mass Equation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 104-125
- Print publication:
- 1965
-
- Article
- Export citation
II.—The Effect of Concentration on the Terminal Fall Velocity of Particles in Suspension*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 9-24
- Print publication:
- 1965
-
- Article
- Export citation
The Stress on the boundary of an elastic half-plane in which body forces are acting
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 48-54
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
IX.—Orthogonal Boolean Matrices*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 126-135
- Print publication:
- 1965
-
- Article
- Export citation
Proximate order (R) of entire functions represented by Dirichlet series (IV)
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 15-18
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
IV.—The Stress in the Vicinity of an Infinite Row of Collinear Cracks in an Elastic Body*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 39-49
- Print publication:
- 1965
-
- Article
- Export citation
A Note on the Hardy-Hille and Mehler formulas
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-60
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
Inequalities involving the genus of a graph and its thicknesses†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 19-21
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
Two integral transform pairs involving hypergeometric functions†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 42-44
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
PRM volume 67 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1965
-
- Article
-
- You have access
- Export citation
GMJ volume 7 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
Lucas and fibonacci numbers and some diophantine Equations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 24-28
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
VI.—Neumann-Series Solutions of the Ellipsoidal Wave Equation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 69-77
- Print publication:
- 1965
-
- Article
- Export citation
XI.—Matrix Analysis of Beam-Columns by the Method of Finite Elements*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 156-173
- Print publication:
- 1965
-
- Article
- Export citation
III.—The Eigenvalue Problem for Boolean Matrices*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 25-38
- Print publication:
- 1965
-
- Article
- Export citation
The spectra of compact operators in Hilbert spaces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 34-38
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
A Note on an asymmetric mixed boundary value problem for a half space with a cylindrical cavity
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 45-47
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
I.—On the Use of Stress Functions for Solving Problems in Linear Viscoelasticity Theory that Involve Moving Boundaries*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-8
- Print publication:
- 1965
-
- Article
- Export citation
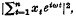 , plays an important part in methods of making inferences about the structure of {x
, plays an important part in methods of making inferences about the structure of {x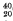 Ca. In the region of greater
Ca. In the region of greater 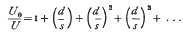

 be an entire
be an entire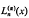 and
and