Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
JAZ volume 5 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
On symmetry in periodic solutions of hamiltonian systems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 463-486
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
Pascal's theorem in n–space*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-408
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
On digital distribution in some integer sequences
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-330
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
Serial dependence of a Markov process
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-314
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
An example of a function with non-analytic iterates
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 388-392
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
The propagation of plane waves in plastic solids
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-364
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
On the rate of convergence of waiting times
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-373
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
On functions of bounded ω-variation, II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 380-387
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
Integral operator methods for generalized axially symmetric potentials in (n+1) variables*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-348
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
On the completeness of Galois theories
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 374-379
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
On fourier transforms of radial functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-298
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
Boolean powers of simple groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-324
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
Topological wreath products
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 396-400
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
Remark on the defining relation of the σ-symbols
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-395
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
Schreier systems in free products
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 2 / July 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 61-79
- Print publication:
- July 1965
-
- Article
-
- You have access
- Export citation
Affine semigroups over an arbitrary field†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 2 / July 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 80-92
- Print publication:
- July 1965
-
- Article
-
- You have access
- Export citation
Some integrability theorems
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 2 / July 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 101-108
- Print publication:
- July 1965
-
- Article
-
- You have access
- Export citation
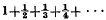
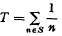
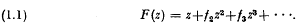


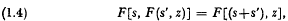
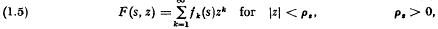
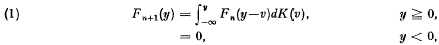

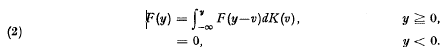
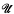 the class of functions
the class of functions 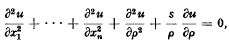
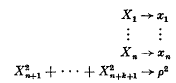
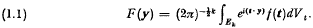

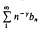

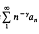 n
n