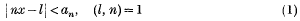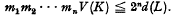Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
Surface waves over a submerged circular cylinder
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 235-245
- Print publication:
- December 1965
-
- Article
- Export citation
On linear relations between roots of unity
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-117
- Print publication:
- December 1965
-
- Article
- Export citation
On the dimension of a graph
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-122
- Print publication:
- December 1965
-
- Article
- Export citation
Lattice coverings of five space by spheres
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-150
- Print publication:
- December 1965
-
- Article
- Export citation
Metric simultaneous diophantine approximation (II)
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-127
- Print publication:
- December 1965
-
- Article
- Export citation
MTK volume 12 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1965
-
- Article
-
- You have access
- Export citation
Oscillatory motion of an elastico-viscous liquid contained between two coaxial cylinders
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 246-256
- Print publication:
- December 1965
-
- Article
- Export citation
Oscillating viscous flows
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-175
- Print publication:
- December 1965
-
- Article
- Export citation
Three proofs of Minkowski's second inequality in the geometry of numbers
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 453-462
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
Altitudes of a general n–simplex*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-415
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
A moment problem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 487-490
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
Gravity effects in the water entry problem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 427-433
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
Corrigendum
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, p. 512
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
On the strength of packed spheres
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 443-452
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
Invariant measures on double coset spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 495-505
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
A bound for the class of certain nilpotent groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 506-511
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
A note on pre-interior operators
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 491-494
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
A queueing system with moving average input process and batch arrivals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 434-442
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation
Irreducible continua and generalization of hereditarily unicoherent continua by means of membranes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 4 / November 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-426
- Print publication:
- November 1965
-
- Article
-
- You have access
- Export citation