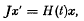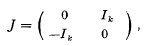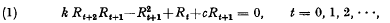Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Diffusion from an elevated point source into a turbulent atmosphere
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-57
- Print publication:
- June 1965
-
- Article
- Export citation
A note on linear transversely isotropic fluids
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 27-29
- Print publication:
- June 1965
-
- Article
- Export citation
Cubic Diophantine equations: the necessary congruence condition
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-38
- Print publication:
- June 1965
-
- Article
- Export citation
Scalar matrix quadratic residues
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-96
- Print publication:
- June 1965
-
- Article
- Export citation
On the large sieves of Linnik and Rényi
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1965
-
- Article
- Export citation
On the unsteady motion of a rotating fluid in a cavity
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-106
- Print publication:
- June 1965
-
- Article
- Export citation
A theorem on convex kernels
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-93
- Print publication:
- June 1965
-
- Article
- Export citation
Cubic Diophantine equations: a supplementary congruence condition
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-48
- Print publication:
- June 1965
-
- Article
- Export citation
On badly approximable numbers
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-20
- Print publication:
- June 1965
-
- Article
- Export citation
Metrics for sets of convex bodies
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-88
- Print publication:
- June 1965
-
- Article
- Export citation
On irredundant components of the kernel of an ideal
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-72
- Print publication:
- June 1965
-
- Article
- Export citation
Plasticity theory and multipolar continuum mechanics
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-26
- Print publication:
- June 1965
-
- Article
- Export citation
Eigen-functions for the strip problem
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-64
- Print publication:
- June 1965
-
- Article
- Export citation
MTK volume 12 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1965
-
- Article
-
- You have access
- Export citation
A characterisation of the moebius and similarity groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-240
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
A theorem in asymptotic number theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 196-206
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
On the stability of linear canonical systems with periodic coefficients
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-195
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
Eigenfunctions of plane elastostatics III the Wedge
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-257
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
Infinite linear systems with homogeneous kernel of degree –1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-168
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
The stability of harrod's growth model of an economy
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-215
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
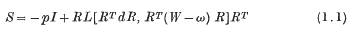
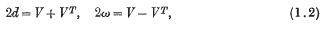
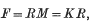
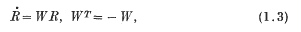
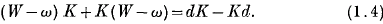
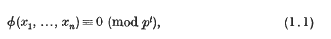


 be a non-empty subset of the set of integers
be a non-empty subset of the set of integers
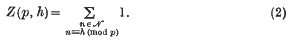
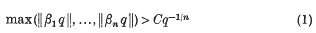
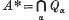 is called the
is called the 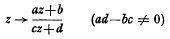
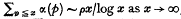 , where if ρ = 1 then
, where if ρ = 1 then 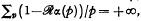 then
then 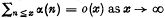 . He applied this result to several problems such as uniform distribution (mod 1) of certain types of sequences.
. He applied this result to several problems such as uniform distribution (mod 1) of certain types of sequences.