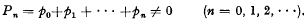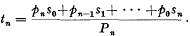Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
Eigenfunctions of plane elastostatics III the Wedge
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-257
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
Infinite linear systems with homogeneous kernel of degree –1
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-168
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
The stability of harrod's growth model of an economy
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-215
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
Spans of translates in Lp(G)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-233
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
A note on cumulative sums of markovian variables
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 285-287
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
Neo-Lorentzian relativity
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-284
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
A Problem in shock wave decay
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-272
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
On the radical of a ring with minimum condition
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 2 / May 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 234-236
- Print publication:
- May 1965
-
- Article
-
- You have access
- Export citation
Self-polar double configurations in projective geometry
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 69-75
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
Monotone mappings in topological linear spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-35
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
A second look at a queueing system with moving average input process
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-106
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
Certain representation algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-99
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
JAZ volume 5 issue 1 Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
Sur l'unicité des solutions de l'équation d'abel-schröder et l'itération continue
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 36-47
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
On the stability of a second-order differential equation
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-16
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
A generalisation of the radon-nikodym theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-24
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
Arithmetic properties of lacunary power series with integral coefficients
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-64
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation
Absolute regularity of the Nörlund mean
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation


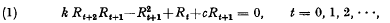
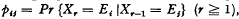 , and an initial probability distribution given by the vector
, and an initial probability distribution given by the vector 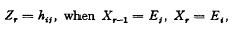
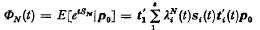
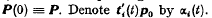 .
.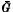 the closure of
the closure of 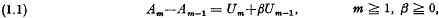
 over a field
over a field  . Λ is made the basis of an algebra
. Λ is made the basis of an algebra  over the complex numbers
over the complex numbers 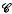 , called the representation algebra, in which multiplication corresponds to the tensor product of representations and addition to direct sum. Green [5] has shown that if char
, called the representation algebra, in which multiplication corresponds to the tensor product of representations and addition to direct sum. Green [5] has shown that if char 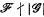 (the non-modular case) or if
(the non-modular case) or if 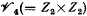 or
or 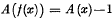

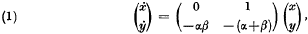
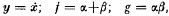
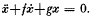
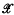 be a space of points
be a space of points  a σ-field of subsets of
a σ-field of subsets of