Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
On minimal n-universal graphs
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 32-33
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
PRM volume 67 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1965
-
- Article
-
- You have access
- Export citation
GMJ volume 7 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
Generalizations of a well-known result in matrix theory
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 29-31
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
PRM volume 67 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1965
-
- Article
-
- You have access
- Export citation
Continuous sums of measures and continuous spectra
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 9-14
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
X.—Nitrogen Dioxide Vapour and the Creation of Condensation Nuclei*†
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 136-155
- Print publication:
- 1965
-
- Article
- Export citation
An extension of a theorem of Gordon
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-41
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
On Lattice Complements
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 22-23
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
VII.—Jacobians of Transformations involving Orthogonal Matrices*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 81-103
- Print publication:
- 1965
-
- Article
- Export citation
V.—Bifurcation of a Parallel-Plate Waveguide by a Unidirectionally Conducting Screen*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 1 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. 50-68
- Print publication:
- 1965
-
- Article
- Export citation
PRM volume 67 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 2 / 1965
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1965
-
- Article
-
- You have access
- Export citation
On the commutativity of the radical of a group algebra
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 1 / January 1965
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-8
- Print publication:
- January 1965
-
- Article
-
- You have access
- Export citation
The second moment of the complexity of a graph
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 95-98
- Print publication:
- December 1964
-
- Article
- Export citation
MTK volume 11 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1964
-
- Article
-
- You have access
- Export citation
A mixed boundary value problem of two-dimensional elasticity theory
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-154
- Print publication:
- December 1964
-
- Article
- Export citation
Index to volume 11
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, p. 185
- Print publication:
- December 1964
-
- Article
- Export citation
Cubic congruences
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-150
- Print publication:
- December 1964
-
- Article
- Export citation
A note on a problem of littlewood about diophantine approximation
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-141
- Print publication:
- December 1964
-
- Article
- Export citation
The stresses in an infinite strip containing a circular inclusion
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-170
- Print publication:
- December 1964
-
- Article
- Export citation

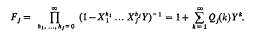
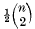 No moments higher than the first were known in general and they remarked in [4] that even “the second would be worth knowing”. The main object in this paper is to derive a formula for the second moment of
No moments higher than the first were known in general and they remarked in [4] that even “the second would be worth knowing”. The main object in this paper is to derive a formula for the second moment of 