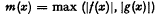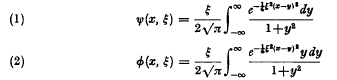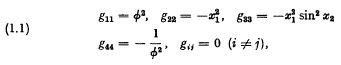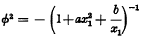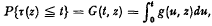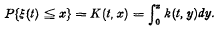Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
Cubic congruences
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-150
- Print publication:
- December 1964
-
- Article
- Export citation
A note on a problem of littlewood about diophantine approximation
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-141
- Print publication:
- December 1964
-
- Article
- Export citation
The stresses in an infinite strip containing a circular inclusion
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-170
- Print publication:
- December 1964
-
- Article
- Export citation
The number of plane trees with a given partition
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- December 1964
-
- Article
- Export citation
The amount of overlapping in partial coverings of space by equal spheres
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-184
- Print publication:
- December 1964
-
- Article
- Export citation
A note on the cyclotomic polynomial
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-136
- Print publication:
- December 1964
-
- Article
- Export citation
The effect of diffusion in the mean wind direction in atmospheric turbulence
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-124
- Print publication:
- December 1964
-
- Article
- Export citation
Some thermoelastic stress distributions in an infinite solid and a thick plate containing penny-shaped cracks
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-118
- Print publication:
- December 1964
-
- Article
- Export citation
On the quintic character of 2
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-130
- Print publication:
- December 1964
-
- Article
- Export citation
On normaliser preserving lattice isomorphisms between nilpotent groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 454-469
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Finite groups with a nilpotent maximal subgroup
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-451
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Lattic isomorphisms of lie algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 470-475
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Solution of a generalized Schroeder equation in two variables
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 410-417
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
An inequality for a pair of polynomials that are relatively prime
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-420
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Voigt profile functions in the complex domain
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 476-488
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
On a type of Riemannian space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-424
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Inequalities for ideal bases in algebraic number fields
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-448
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Translates of L∞ functions and of bounded measures
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-409
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
On the distribution of the time to first emptiness of a store with stochastic input
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 506-517
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
Groups with one defining relator
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 4 / Issue 4 / November 1964
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-392
- Print publication:
- November 1964
-
- Article
-
- You have access
- Export citation
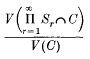
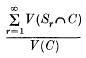
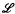 (
(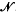
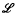 (
(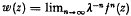 . Here
. Here