Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
On commutation semigroups of a group
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 36-45
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
On n+1 intersecting hyperspheres in n-space†
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Bisimple ω-Semigroups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 160-167
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
The Reissner-Sagoci problem †
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 136-144
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
GMJ volume 7 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
Certain fundamental congruences on a regular semigroup†
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 145-159
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
Adjunction of roots to nilpotent groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 109-118
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
GMJ volume 7 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
On integral equations involving Whittaker's function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 125-127
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
Isomorphic congruence groups and Hecke operators
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, p. 168
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
Generalized Cesaro means of order −1
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-124
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
The maxit and minit of a ring
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 3 / January 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 128-135
- Print publication:
- January 1966
-
- Article
-
- You have access
- Export citation
The densest double lattice packing of four-spheres
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-142
- Print publication:
- December 1965
-
- Article
- Export citation
An investigation of the elastic strip and the annulus
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-200
- Print publication:
- December 1965
-
- Article
- Export citation
A minimal density plane covering problem
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 226-234
- Print publication:
- December 1965
-
- Article
- Export citation
Convection in a self-gravitating fluid sphere
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-137
- Print publication:
- December 1965
-
- Article
- Export citation
Index to volume 12
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, p. 257
- Print publication:
- December 1965
-
- Article
- Export citation
Biquadratic congruences
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-160
- Print publication:
- December 1965
-
- Article
- Export citation
The distribution of solutions of congruences
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 176-192
- Print publication:
- December 1965
-
- Article
- Export citation
On the large sieve
-
- Journal:
- Mathematika / Volume 12 / Issue 2 / December 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
- Print publication:
- December 1965
-
- Article
- Export citation
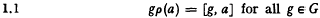
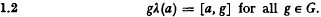

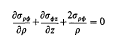
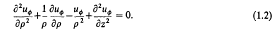
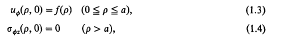
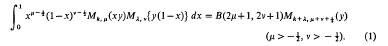
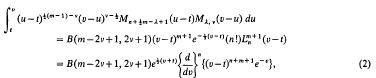
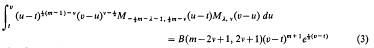
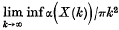 . The problem is to find the exact lower bound of the lower density for any saturated set of circles. We show that it is φ/(6√3) provided the circles are disjoint. The general case, when they may overlap, remains unsolved.
. The problem is to find the exact lower bound of the lower density for any saturated set of circles. We show that it is φ/(6√3) provided the circles are disjoint. The general case, when they may overlap, remains unsolved.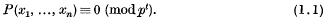
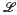
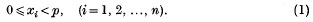
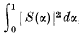 where
where 