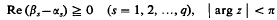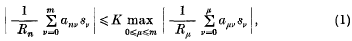Refine search
Actions for selected content:
28981 results in Differential and integral equations, dynamical systems and control theory
Linear operators which commute with translations. Part II: Applications of the representation theorems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-350
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
On integral operators associated with Poisson transforms and the operator Hα
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-272
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
On metabelian groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 362-368
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
On the complete integral closure of an integral domain
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-361
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
Linear operators which commute with translations. Part I: Representation theorems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-327
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
String vibrating at finite amplitude
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-384
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
Interval semirings on R1 with ordinary multiplication
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-288
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
GMJ volume 7 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
Congruences on a bisimple ω-semigroup
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 184-192
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
The structure of cancellative power-free groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-206
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
A remark on the distributive law for an ideal in a commutative ring
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 193-198
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
Note on the region of overconvergence of Dirichlet series with Ostrowski gaps
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 169-173
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
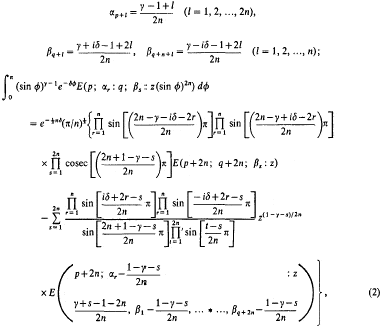
Integrals involving E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 174-177
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
The semigroup of doubly-stochastic matrices
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 178-183
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
GMJ volume 7 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
Non-cancellative power-free groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 7 / Issue 4 / July 1966
- Published online by Cambridge University Press:
- 18 May 2009, pp. 207-212
- Print publication:
- July 1966
-
- Article
-
- You have access
- Export citation
An inequality for sequence transformations
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 26-41
- Print publication:
- June 1966
-
- Article
- Export citation
Reducible convex sets
-
- Journal:
- Mathematika / Volume 13 / Issue 1 / June 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-50
- Print publication:
- June 1966
-
- Article
- Export citation