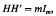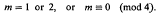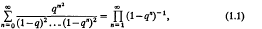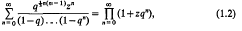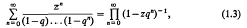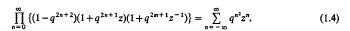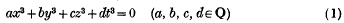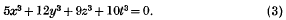Refine search
Actions for selected content:
28981 results in Differential and integral equations, dynamical systems and control theory
XXIII.—Autocorrelation in Black Body Radiation and in Density Fluctuation Waves in Liquids*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 289-302
- Print publication:
- 1967
-
- Article
- Export citation
A new class of Hadamard matrices
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-62
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
PRM volume 67 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1967
-
- Article
-
- You have access
- Export citation
XVII.—Generalized Hypo-Elasticity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 220-230
- Print publication:
- 1967
-
- Article
- Export citation
GMJ volume 8 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
PRM volume 67 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1967
-
- Article
-
- You have access
- Export citation
XXIV.—The Spirit of Science
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 303-308
- Print publication:
- 1967
-
- Article
- Export citation
XIV.—On Eigenvectors of Boolean Matrices*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 196-204
- Print publication:
- 1967
-
- Article
- Export citation
Enumerative proofs of certain q-identities
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 33-40
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
XXII.—Tensor Fields and Connections on Cross-Sections in the tangent bundle of a differentiable manifold*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 277-288
- Print publication:
- 1967
-
- Article
- Export citation
Enumeration of self-converse digraphs
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-157
- Print publication:
- December 1966
-
- Article
- Export citation
Lagrange's theorem for weak functions
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-171
- Print publication:
- December 1966
-
- Article
- Export citation
The Steiner point of a closed hypersurface
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 181-188
- Print publication:
- December 1966
-
- Article
- Export citation
Index to volume 13
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, p. 217
- Print publication:
- December 1966
-
- Article
- Export citation
MTK volume 13 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1966
-
- Article
-
- You have access
- Export citation
On wing–body interference in supersonic flow
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 121-139
- Print publication:
- December 1966
-
- Article
- Export citation
Some applications of Bombieri's theorem
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 196-203
- Print publication:
- December 1966
-
- Article
- Export citation
On the projection of Souslin sets
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-150
- Print publication:
- December 1966
-
- Article
- Export citation
Some basic properties of penny-shaped cracks
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-180
- Print publication:
- December 1966
-
- Article
- Export citation
On the Hasse principle for cubic surfaces
-
- Journal:
- Mathematika / Volume 13 / Issue 2 / December 1966
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-120
- Print publication:
- December 1966
-
- Article
- Export citation