Refine search
Actions for selected content:
28978 results in Differential and integral equations, dynamical systems and control theory
A note on doubly transitive groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-451
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
On the lattice equivalence of topological spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 495-511
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
A note on a result of Mahler's
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-401
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
A converse to Lebesgue's dominated convergence theorem
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 477-479
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Summation of infinite series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 470-476
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
On Rotor calculus, I
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 402-423
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Involutory automorphisms of groups of odd order
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 480-494
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
On Rotor calculus, II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 424-448
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Finite simple groups with nilpotent third maximal subgroups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 466-469
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Generalization of a theorem of P. D. Finch's on integration of set-functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 460-465
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Another Law for the 3-Metabelian Groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, p. 512
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Rational polygons
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 452-459
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Forced motion of a charged particle in a magnetic field
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-398
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Report of the Australian Mathematical Society
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-258
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
Minimal dependent sets
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-262
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
Linear operators which commute with translations. Part II: Applications of the representation theorems
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-350
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
On integral operators associated with Poisson transforms and the operator Hα
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-272
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
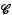 of its subsets which has the properties (i) arbitrary set intersections of members of
of its subsets which has the properties (i) arbitrary set intersections of members of 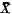 denotes the closure of
denotes the closure of 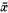 . The pair (
. The pair (
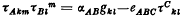
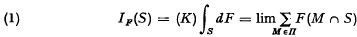
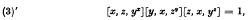

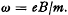 .
.