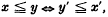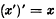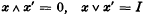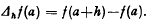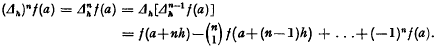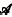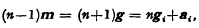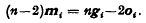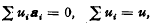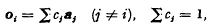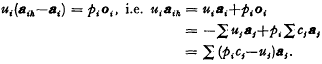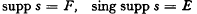Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
JAZ volume 6 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 2 / May 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- May 1966
-
- Article
-
- You have access
- Export citation
Radially symmetric distribution of matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 2 / May 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-156
- Print publication:
- May 1966
-
- Article
-
- You have access
- Export citation
A convolution semigroup of modular functions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 2 / May 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-255
- Print publication:
- May 1966
-
- Article
-
- You have access
- Export citation
On a characterisation of conformally-flat Riemannian spaces of class one
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 2 / May 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 172-178
- Print publication:
- May 1966
-
- Article
-
- You have access
- Export citation
Self-polar double-N's defined by certain pairs of normal rational curves
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 2 / May 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 210-220
- Print publication:
- May 1966
-
- Article
-
- You have access
- Export citation
Power-associative regular real normed algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 2 / May 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-209
- Print publication:
- May 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Perspective simplexes †
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-17
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
A generalisation of Lorentz-equivalence in a substratum theory
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 101-105
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Algorithms for generalized stability numbers of tree graphs
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 89-100
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Congruence relations on orthomodular lattices
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 46-54
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Propagation of elastic waves
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-64
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Infinite capacity storage processes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 30-35
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
A theorem on a finite difference operator and its connection with the Poisson distribution
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-29
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Some geometric extremal problems*
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 122-128
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
The modular representation algebra of groups with Sylow 2-subgroup Z2 × Z2
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 76-88
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
A special simplex †
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-24
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
JAZ volume 6 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Lattice isomorphisms of associative algebras
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 106-121
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
Supports and singular supports of pseudomeasures
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-75
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
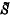 be the collection of all normalized non-negative Borel measures on S. It is well-known that
be the collection of all normalized non-negative Borel measures on S. It is well-known that 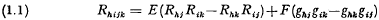
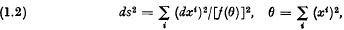
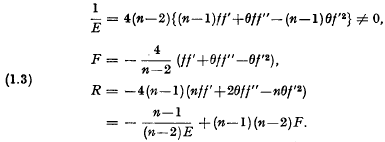
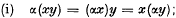

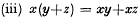
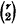 centres of perspectivity (c.p.) lie in an [r−2] (say
centres of perspectivity (c.p.) lie in an [r−2] (say 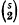 c.p. lie in
c.p. lie in