A group G is called a c-group if each of its subnormal subgroups is characteristic in G. It is the object of this note to give a characterization of finite solvable c-groups.

Let E be a real Banach space. The set of all continuous linear mappings of E into E is a Banach algebra under the usual algebraic operations and the operator bound as norm. We denote this Banach algebra by ℒ, if E is a separate Hilbert space.

Let f = f(x) = f(x1, x2,…, xn) be an indefinite n-ary quadratic form of determinant det (f); that is, f(x) = x' Ax where A is a real symmetric matrix with determinant det (f). Such a form is said to take the value v if there exists integral x ≠ 0 such that f(x) = v.

Let G be a group and let Ω(G) denote the semigroup of all mappings of G into G with the usual composition of mappings as multiplication, namely g(θ1θ22) = (gθ1)θ2.

It is well known that the problem of determining the most economical covering of n-dimensional Eucidean space, by equal spheres whose centres form a lattice, may be formulated in terms of positive definite quadratic forms, as follows: Let

be positive definite, and

For real α, set

(the minimum being taken over integral x),

Let {f(n)} be a linear recurrence of order two, i.e.

for all positive integers n.

Let G be a locally compact Abelian Hausdorff group (abbreviated LCA group); let X be its character group and dx, dx be the elements of the normalised Haar measures on G and X respectively. If 1 < p, q < ∞, and Lp(G) and Lq(G) are the usual Lebesgue spaces, of index p and q respectively, with respect to dx, a multiplier of type (p, q) is defined as a bounded linear operator T from Lp(G) to Lq(G) which commutes with translations, i.e. τxT = Tτx for all x ∈ G, where τxf(y) = f(x+y). The space of multipliers of type (p, q) will be denoted by Lqp. Already, much attention has been devoted to this important class of operators (see, for example, [3], [4], [7]).

In 1959, Professor N. A. Court [2] generated synthetically a twisted cubic C circumscribing a tetrahedron T as the poles for T of the planes of a coaxal family whose axis is called the Lemoine axis of C for T. Here is an analytic attempt to relate a normal rational curve rn of order n, whose natural home is an n-space [n], with its Lemoine [n—2] L such that the first polars of points in L for a simplex S inscribed to rn pass through rn anf the last polars of points on rn for S pass through L. Incidently we come across a pair of mutually inscribed or Moebius simplexes but as a privilege of odd spaces only. In contrast, what happens in even spaces also presents a case, not less interesting, as considered here.

This is the first of several papers which grew out of an attempt to provide C (X, Y), the family of all continuous functions mapping a topological space X into a topological space Y, with an algebraic structure. In the event Y has an algebraic structure with which the topological structure is compatible, pointwise operations can be defined on C (X, Y). Indeed, this has been done and has proved extremely fruitful, especially in the case of the ring C (X, R) of all continuous, real-valued functions defined on X [3]. Now, one can provide C(X, Y) with an algebraic structure even in the absence of an algebraic structure on Y. In fact, each continuous function from Y into X determines, in a natural way, a semigroup structure for C(X, Y). To see this, let ƒ be any continuous function from Y into X and for ƒ and g in C(X, Y), define ƒg by each x in X.

A sequence of integers 0 <a1 < a2 <… no term of which divides any other will be called a primitive sequence. Throughout this paper c1, c2,… will denote suitable positive absolute constants. Behrend [1] proved that for every primitive sequence

Although varieties of groups can in theory be determined as well by the identical relations which the groups all satisfy as by some structural property inherited by subgroups, factor groups and cartesian products which the groups have in common, it seems in practice just as hard to answer questions about properties of a group from knowledge of identical relations as it is from, say, a presentation. Many of the important questions connected with Burnside's problems exemplify this difficulty: we still do not know if there is a bound on the derived length of finite groups of exponent 4, nor whether there is a bound on the nilpotency class of finite groups of exponent p (p ≧ 5, a fixed prime).

Consider an m × n rectangular array whose m rows are permutations of 1, 2, …, n. Such an array will be called a constant-sum array if the sum of the elements in each column is the same (and equal to ½m (n+1)). An example of a 3×9 constant-sum array is In contrast to a Latin rectangle, elements in the same column of a constantsum array may be equal. It will be convenient to assume arrays normalised in the sense that the columns are arranged so that, as in (1), the first row is in the standard order 1, 2, …, n.

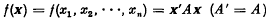
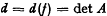
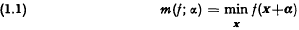
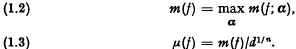
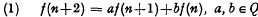
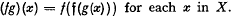
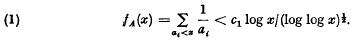
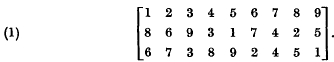
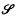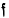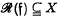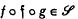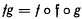This is a continuation of [5] and we begin by recalling two definitions and a result of that paper which are needed here. Let be a family of functions with domains contained in a set X and ranges contained in a set Y and let be a function with domain D()= Y and range with the property for each pair of elements ƒ and g of . Since the composition operation is associative, is a semigroup if for ƒ and g in , we define the product ƒg by .

Let E be a vector lattice in the sense of Birkhoff [1]. We use the following notations:

Suppose that the real-valued function ƒ(t) is positive, continuous and monotonic increasing for t ≧ t0. If x = x (t) is a solution of the equation for for t ≧ t0, it is known that the solution x(t) oscillates infinitely often as t → ∞ and that the successive maxima of |x(t)| decrease, with increasing t. In particular x(t) is bounded as t → ∞.

The purpose of this article is to present some results on varieties of metabelian p-groups, nilpotent of class c, with the prime p greater than c. After some preliminary lemmas in § 3, it is established in § 4, Theorem 3, that there is a simple basis for the laws of such a variety, and this basis is explicitly stated. This allows the description of the lattice of such varieties, and in § 5, Theorem 4, it is shown that each such variety has a two-generator member which generates it; this is established by the help of Theorem 5, which states that each critical group is a two-generator group, and Theorem 6, which gives explicitly the varieties generated by the proper subgroups, by the proper quotient groups, and by the proper factor groups of such a critical group.

Gy. Soos [1] and B. Gupta [2] have discussed the properties of Riemannian spaces Vn (n > 2) in which the first covariant derivative of Weyl's projective curvature tensor is everywhere zero; such spaces they call Protective-Symmetric spaces. In this paper we wish to point out that all Riemannian spaces with this property are symmetric in the sense of Cartan [3]; that is the first covariant derivative of the Riemann curvature tensor of the space vanishes. Further sections are devoted to a discussion of projective-symmetric af fine spaces An with symmetric af fine connexion. Throughout, the geometrical quantities discussed will be as defined by Eisenhart [4] and [5].

In this paper we investigate finite metabelian p-groups from the point of view of varieties and identical relations. In other words we shall be interested in those properties of such groups which are preserved under the operations of fonning direct products, taking subgroups and taking factor groups. Ideally one would like to characterize such properties in terms of numerical invariants and with the sole restriction that the p-group in question have class less than p we accomplish this.