Refine search
Actions for selected content:
28986 results in Differential and integral equations, dynamical systems and control theory
A note on vector lattices
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 1 / February 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 32-38
- Print publication:
- February 1967
-
- Article
-
- You have access
- Export citation
A stability result for the linear differential equation x”+f(t)x = 0
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 1 / February 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-8
- Print publication:
- February 1967
-
- Article
-
- You have access
- Export citation
On varieties of metabelian p-groups, and their laws
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 1 / February 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-80
- Print publication:
- February 1967
-
- Article
-
- You have access
- Export citation
Projective-symmetric spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 1 / February 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 48-54
- Print publication:
- February 1967
-
- Article
-
- You have access
- Export citation
On metabelian p-groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 1 / February 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-63
- Print publication:
- February 1967
-
- Article
-
- You have access
- Export citation
JAZ volume 7 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 7 / Issue 1 / February 1967
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1967
-
- Article
-
- You have access
- Export citation
XIX.—On the Determination of the General Term in Green-type Expansions*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 243-255
- Print publication:
- 1967
-
- Article
- Export citation
XX.—Some New Results in Maximum Likelihood Factor Analysis*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 256-264
- Print publication:
- 1967
-
- Article
- Export citation
Some integral equations involving finite parts of divergent integrals
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 50-54
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
XIII.—The Generating Function of Solid Partitions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 185-195
- Print publication:
- 1967
-
- Article
- Export citation
Index
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 353-354
- Print publication:
- 1967
-
- Article
- Export citation
XVI.—On Certain Numerical Coefficients Associated with Partitions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 215-219
- Print publication:
- 1967
-
- Article
- Export citation
XVIII.—The Solution of Equations in a Lattice.
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 231-242
- Print publication:
- 1967
-
- Article
- Export citation
XV.—A Matrix Analogue of the Integral

-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 205-214
- Print publication:
- 1967
-
- Article
- Export citation
PRM volume 67 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 3 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1967
-
- Article
-
- You have access
- Export citation
Compact linear operators from an algebraic standpoint
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 41-49
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
XXI—The Whittaker-Hill Equation and the Wave Equation in Paraboloidal Co-ordinates
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. 265-276
- Print publication:
- 1967
-
- Article
- Export citation
PRM volume 67 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 67 / Issue 4 / 1967
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1967
-
- Article
-
- You have access
- Export citation
Proof of a conjecture of Ramanujan
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 14-32
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
Naturally ordered bands
-
- Journal:
- Glasgow Mathematical Journal / Volume 8 / Issue 1 / January 1967
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-58
- Print publication:
- January 1967
-
- Article
-
- You have access
- Export citation
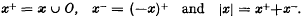
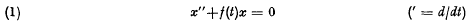
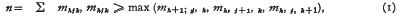
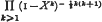 , but this is now known to be false. We write η(
, but this is now known to be false. We write η(