Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
JAZ volume 3 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
On the integration processes of A. Huťa
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 202-206
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
Linear groups analogous to permutation groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 180-184
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
The single server queueing system with Non-recurrent input-process and Erlang service time
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 220-236
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
On T-systems of groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 172-179
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
Weak convergence of vector-valued series and integrals
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-166
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
Coefficients for the study of Runge-Kutta integration processes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-201
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
The lifting two-dimensional aerofoil between slotted walls
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-219
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
Minimal Hausdorff and maximal compact spaces
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 2 / May 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 167-171
- Print publication:
- May 1963
-
- Article
-
- You have access
- Export citation
The elastodynamics of moving loads, Part 1: The field of a semi-infinite line load moving on the surface of an elastic solid with constant supersonic velocity
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-92
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
A note on a method of Milne-Thomson
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-98
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
Two non-linear birth and death processes
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 104-116
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
Tetrads of Möbius tetrahedra
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 68-78
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
On supplements in finite groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 63-67
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
The convergence of Rayleigh-Ritz approximations in hydrodynamics
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 99-103
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
The structure of cyclic paired-comparison designs
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-127
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
On the conjugacy classes in the unitary, symplectic and orthogonal groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-62
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
JAZ volume 3 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 3 / Issue 1 / February 1963
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- February 1963
-
- Article
-
- You have access
- Export citation
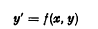
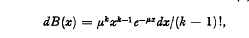
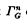 denote the set of all generating
denote the set of all generating 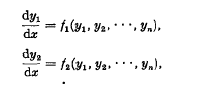
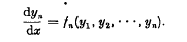
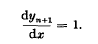
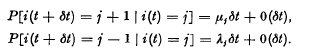
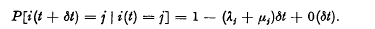
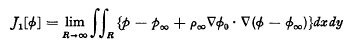
 comparisons. There are frequent occasions when it si desirable to make only a fraction
comparisons. There are frequent occasions when it si desirable to make only a fraction 