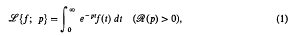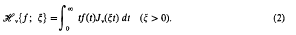Refine search
Actions for selected content:
28970 results in Differential and integral equations, dynamical systems and control theory
GMJ volume 5 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
Group Algebras With Central Radicals
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-108
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
On a set of normal subgroups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-146
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
On the natural representation of the symmetric groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-136
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
Some Series and Recurrence Relations for MacRobert's E-Function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 116-117
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
I.—Focusing of Electron Beams in Crossed Static Electric and Magnetic Fields*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 1 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-19
- Print publication:
- 1962
-
- Article
- Export citation
PRM volume 66 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 2 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1962
-
- Article
-
- You have access
- Export citation
VII.–The Effect of the Transport of Heat on the Rate of Evaporation of Small Droplets‡ I. Evaporation into a Large Excess of a Gas
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 2 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 65-80
- Print publication:
- 1962
-
- Article
- Export citation
II.—Spontaneous Fission Rates and the Role of the “Excess” Neutrons in Heavy Nuclei*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 1 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 20-32
- Print publication:
- 1962
-
- Article
- Export citation
IX.—Possible Applications of Coincidence Counter Techniques in Optical Intensity Correlation Studies*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 2 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 93-110
- Print publication:
- 1962
-
- Article
- Export citation
VIII.—Theoretical Expressions for Relaxation Effects in the Thermal Conductivity of Gases as Measured in the Modified Co-axial Cylinder Apparatus of Callear and Robb
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 2 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 81-92
- Print publication:
- 1962
-
- Article
- Export citation
Summation of a series of products of E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 118-120
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
PRM volume 66 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 1 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1962
-
- Article
-
- You have access
- Export citation
The centre of a hereditary local ring
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 101-102
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
A Relation between Laplace and Hankel Transforms
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 114-115
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
PRM volume 66 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 1 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1962
-
- Article
-
- You have access
- Export citation
VI.—Endomorphisms of Abstract Algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 1 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 53-64
- Print publication:
- 1962
-
- Article
- Export citation
X.—Remarks on Coincidence Experiments with Visible Light*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 2 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 111-115
- Print publication:
- 1962
-
- Article
- Export citation
On P. Hall's Generalisation of a Theorem of Frobenius
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 3 / January 1962
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-100
- Print publication:
- January 1962
-
- Article
-
- You have access
- Export citation
V.—A Search for n-γ Coincidences from a Po-Li Neutron Source
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 66 / Issue 1 / 1962
- Published online by Cambridge University Press:
- 14 February 2012, pp. 47-52
- Print publication:
- 1962
-
- Article
- Export citation
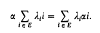

 , a result involving
, a result involving