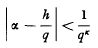Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Arithmetical Functions of a Greatest Common Divisor, III. Cesàro's Divisor Problem
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 5 / Issue 2 / July 1961
- Published online by Cambridge University Press:
- 18 May 2009, pp. 67-75
- Print publication:
- July 1961
-
- Article
-
- You have access
- Export citation
On the non-specialisation of intersections on a singular variety
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-44
- Print publication:
- June 1961
-
- Article
- Export citation
On Kloosterman's sum
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-86
- Print publication:
- June 1961
-
- Article
- Export citation
MTK volume 8 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1961
-
- Article
-
- You have access
- Export citation
A note on the maximum resultant shear in the aeolotropic torsion problem
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-82
- Print publication:
- June 1961
-
- Article
- Export citation
On two-centred expansions in cylindrical polar co-ordinates
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-78
- Print publication:
- June 1961
-
- Article
- Export citation
Cauchy problem for the generalised radially symmetric wave equation
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 66-68
- Print publication:
- June 1961
-
- Article
- Export citation
A note on binary cubic forms
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-62
- Print publication:
- June 1961
-
- Article
- Export citation
Completely aeolotropic cylinders under general lateral loading
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-54
- Print publication:
- June 1961
-
- Article
- Export citation
The real cubic case of Mahler's conjecture
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-57
- Print publication:
- June 1961
-
- Article
- Export citation
Indefinite quadratic Diophantine equations
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-38
- Print publication:
- June 1961
-
- Article
- Export citation
Note on a conjecture of L. A. Santaló
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-65
- Print publication:
- June 1961
-
- Article
- Export citation
Functions continuous and singular with respect to a Hausdorff measure
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-31
- Print publication:
- June 1961
-
- Article
- Export citation
Rational approximation with series
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 107-119
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
Some applications of the Eulerian functions of a finite group
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-59
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
On the Clifford collineation, transform and similarity groups. I.
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 60-79
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
Necessary and sufficient conditions for unitary similarity
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 122-126
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
Acceleration and the “clock paradox”.
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 120-121
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
The inhomogeneous minima of indefinite quadratic forms
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-10
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
On the Clifford collineation, transform and similarity groups. II.
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 1 / April 1961
- Published online by Cambridge University Press:
- 09 April 2009, pp. 80-96
- Print publication:
- April 1961
-
- Article
-
- You have access
- Export citation
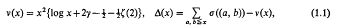
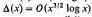 . This estimate was later improved to
. This estimate was later improved to 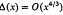 . The precise statement of the result for σ((
. The precise statement of the result for σ((
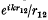 This work formed an extension to that of Carlson and Rushbrooke [2] (also Buehler and Hirschfelder [3]) on the Coulomb Green's function and arose out of considerations of the interaction energy of two charge distributions taking account of electromagnetic retardation. The two-centred expansion obtained in [1] took the form of a double Taylor series, each term being interpreted as a Maxwell multipole—multipole interaction energy between two “charge” distributions coupled through a retarded scalar field. The first few terms in the expansion were also given in spherical polar coordinates.
This work formed an extension to that of Carlson and Rushbrooke [2] (also Buehler and Hirschfelder [3]) on the Coulomb Green's function and arose out of considerations of the interaction energy of two charge distributions taking account of electromagnetic retardation. The two-centred expansion obtained in [1] took the form of a double Taylor series, each term being interpreted as a Maxwell multipole—multipole interaction energy between two “charge” distributions coupled through a retarded scalar field. The first few terms in the expansion were also given in spherical polar coordinates.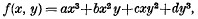

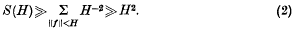
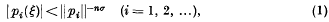
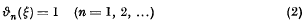
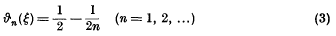
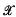 be a plane bounded convex set whose width in the direction φ is
be a plane bounded convex set whose width in the direction φ is 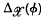 . It has been shown by L. A. Santaló that
. It has been shown by L. A. Santaló that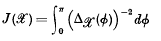
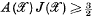 and that equality characterizes triangles. In this note Santaló's conjecture is shown to be true.
and that equality characterizes triangles. In this note Santaló's conjecture is shown to be true.