Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
Jacobians for Measures in Coset Spaces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 4 / September 1960
- Published online by Cambridge University Press:
- 18 May 2009, pp. 208-212
- Print publication:
- September 1960
-
- Article
-
- You have access
- Export citation
Some automorphisms of finite nilpotent groups
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 4 / September 1960
- Published online by Cambridge University Press:
- 18 May 2009, pp. 204-207
- Print publication:
- September 1960
-
- Article
-
- You have access
- Export citation
Some triple integral equations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 4 / September 1960
- Published online by Cambridge University Press:
- 18 May 2009, pp. 200-203
- Print publication:
- September 1960
-
- Article
-
- You have access
- Export citation
JAZ volume 1 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
Conditionally convergent spectral expansions
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-333
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
The characterisation of the normal distribution
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-383
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
Hilbert spaces of generalized functions extending L2, (I)
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-298
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
JAZ volume 1 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b3
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
Polynomial solutions of binomial congruences
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-280
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
Permutational products of groups
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-310
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
Nozzle flows found by the hodograph method. II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-367
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
On well-bounded operators
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-343
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
The numerical solution of integral equations using Chebyshev polynomials
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 344-356
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
Desargues' theorem in n-space
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 3 / August 1960
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-318
- Print publication:
- August 1960
-
- Article
-
- You have access
- Export citation
A combinatorial problem of T. G. Room
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-55
- Print publication:
- June 1960
-
- Article
- Export citation
Incidence matrices
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-49
- Print publication:
- June 1960
-
- Article
- Export citation
Distinct small values of quadratic forms
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-40
- Print publication:
- June 1960
-
- Article
- Export citation
The flow of a conducting fluid past a magnetized cylinder
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-77
- Print publication:
- June 1960
-
- Article
- Export citation
On Stokes flow about a torus
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-92
- Print publication:
- June 1960
-
- Article
- Export citation
The discriminants of relative extensions and the existence of integral bases
-
- Journal:
- Mathematika / Volume 7 / Issue 1 / June 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-22
- Print publication:
- June 1960
-
- Article
- Export citation
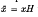 =
= 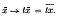 We write, for
We write, for 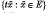 . The measure μ is called
. The measure μ is called 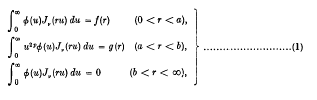
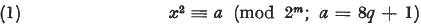
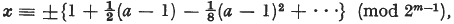
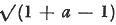 as far as the term of degree
as far as the term of degree  . We shall be concerned here with the structure of such rings
. We shall be concerned here with the structure of such rings 