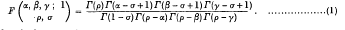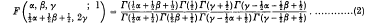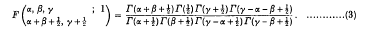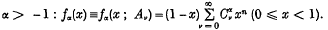Refine search
Actions for selected content:
28962 results in Differential and integral equations, dynamical systems and control theory
On a class of simple rings
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-117
- Print publication:
- December 1958
-
- Article
- Export citation
An application in hydrodynamics of the Green's function of an elastic plate
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 85-92
- Print publication:
- December 1958
-
- Article
- Export citation
On Borel-type methods of summability
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-133
- Print publication:
- December 1958
-
- Article
- Export citation
The Packing of Spheres in the Space lp
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 1 / December 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 22-25
- Print publication:
- December 1958
-
- Article
-
- You have access
- Export citation
Maximum Principles in matrix theory
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 1 / December 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 34-37
- Print publication:
- December 1958
-
- Article
-
- You have access
- Export citation
A recursion formula for the coefficients in an asymptotic expansion
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 1 / December 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 38-41
- Print publication:
- December 1958
-
- Article
-
- You have access
- Export citation
Note on a plane measure problem
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-127
- Print publication:
- December 1958
-
- Article
- Export citation
A doublet technique for solving Oseen's equations of axisymmetric flow
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-140
- Print publication:
- December 1958
-
- Article
- Export citation
Note on a sphere theorem for the axisymmetric stokes flow of a viscous fluid
-
- Journal:
- Mathematika / Volume 5 / Issue 2 / December 1958
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-121
- Print publication:
- December 1958
-
- Article
- Export citation
Infinite Series of E-Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 1 / December 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 26-28
- Print publication:
- December 1958
-
- Article
-
- You have access
- Export citation
A Note on Some Inequalities
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 1 / December 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 7-15
- Print publication:
- December 1958
-
- Article
-
- You have access
- Export citation
GMJ volume 4 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 4 / Issue 1 / December 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- December 1958
-
- Article
-
- You have access
- Export citation
The dynamical stresses produced in a thick plate by the action of surface forces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-163
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
Expansion of an E-function in a series of products of E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 194-195
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
A note on semi-special permutations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 164-169
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
On stratifications of Mittag-Leffler's transcendents
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 170-172
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
Integrals involving hypergeometric functions and E-functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 196-198
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
A note on positive definite matrices
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-175
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
On Tauberian theorems for Abel-Cesàro summability
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 176-181
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
The construction of branched covering Riemann surfaces
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 4 / July 1958
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-207
- Print publication:
- July 1958
-
- Article
-
- You have access
- Export citation
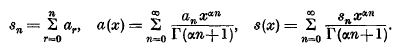
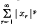 is convergent. Here
is convergent. Here 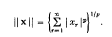
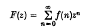
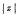 from the behaviour of
from the behaviour of 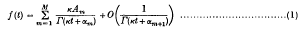
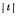 such that
such that