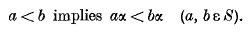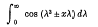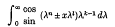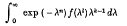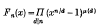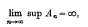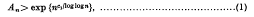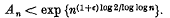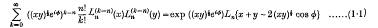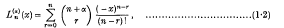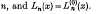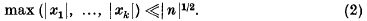Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
On the fractional parts of the powers of a rational number (II)
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-124
- Print publication:
- December 1957
-
- Article
- Export citation
On the solution of problems of dynamic plane elasticity
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 166-168
- Print publication:
- December 1957
-
- Article
- Export citation
An inversion formula for a generalized transform
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 146-155
- Print publication:
- December 1957
-
- Article
- Export citation
On strong Rieszian summability
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 3 / December 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-131
- Print publication:
- December 1957
-
- Article
-
- You have access
- Export citation
The distribution of quadratic residues and non-residues
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
- Print publication:
- December 1957
-
- Article
- Export citation
Groups of order automorphisms of ordered sets
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-50
- Print publication:
- June 1957
-
- Article
- Export citation
Solution of the word problem for certain types of groups II
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 68-90
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
Integrals allied to Airy's integrals
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 91-93
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
On the growth of the cyclotomic polynomial in the interval (0, 1)
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 102-104
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
Uniqueness theorems for thin clamped anisotropic plates
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 70-75
- Print publication:
- June 1957
-
- Article
- Export citation
GMJ volume 3 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
Stress distribution in a notched plate
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-96
- Print publication:
- June 1957
-
- Article
- Export citation
A formula of Bateman
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-101
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
A note on coverings
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
- Print publication:
- June 1957
-
- Article
- Export citation
GMJ volume 3 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
A note on form rings and ideals
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-60
- Print publication:
- June 1957
-
- Article
- Export citation
Bounded representations of integers by quadratic forms
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
- Print publication:
- June 1957
-
- Article
- Export citation
Integration of E-Functions with regard to their parameters
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 94-98
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
The minimum discriminants of quintic fields
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 2 / June 1957
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-67
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
Multiple covering of the plane by circles
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-16
- Print publication:
- June 1957
-
- Article
- Export citation
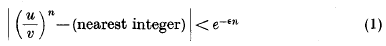
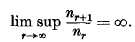
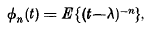
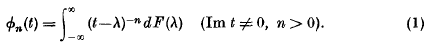
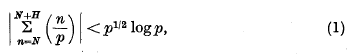
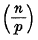 being Legendre's symbol of quadratic character.
being Legendre's symbol of quadratic character.